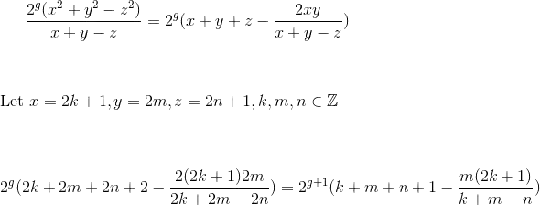Need help with a diophantine expression

Question

I'm faced with this problem. Under what conditions is this expression a positive odd integer:

$$\frac{2^g(x^2+y^2-z^2)}{x+y-z}$$

where $g,x,y,z$ are nonnegative integers. x and z are odd, and y is even.

I see that the power of $2$ that divides $x+y-z$ has to be greater than the power of 2 dividing $x^2+y^2-z^2$. When can this happen?

This is a research-type question, so I'm not looking for a tight answer. Mainly looking for hints on how to tackle this... lines of thought to follow etc. Appreciate any help.

Answer 1

Notice that:

$$x^2+y^2-z^2=(x+y-z)(x+y+z)-2xy$$

So,we have:

EDIT:

Since $g+1 \geq 1$ , $2^{g+1}$ is even. We want $2^{g+1}(k+m+n+1-\frac{m(2k+1)}{k+m-n})$ to be an odd integer.

In order to be odd , $2^{g+1}$ shouldn't exist,so that we don't get an even number.In order to extinguish this amount, the denominator should be a multiple of $2^{g+1}$ ,therefore $k+m-n \equiv 0mod2$ ,so $k+m+n+1 \equiv 1mod2$. It is obvious that with these conditions,we have to check which is the highest power of $2$ that divides $m$.

Finally,it is evident that a necessary condition,so that the expression is an integer is that $k+m-n \mid m(2k+1)$

Answer 2

To begin with note that if you a solution $x,y,z,G$ and an odd number U then clearly $Ux,Uy,Uz,G$ is a solution as well.

Thus we can add the stipulation that we are looking for tuples $x,y,z$ that do not share a common odd factor $U$.

We consider the case of $G > 0$ first.

In that case it becomes clear (through some factoring) that

$$ 2^{g} \frac{2xy}{x + y - z} $$

Must be an odd number. Now since $y$ is an even number it is evident that $y$ can be expressed as $2^rL$ for some odd number L. Therefore we can re-write our expression as

$$ 2^{g + r + 1} \frac{xL}{x + 2^rL - z} $$

So a process for finding solutions becomes apparent. Select a value g and then select a value y. Decompose $y$ into $2^rL$ for odd L. Find a pair of odd numbers (x - z) that do no share factors with L such that $2^{g + r + 1} = x - z + 2^rL$

Which can be done easily by first solving for $x - z$ as a single numerical variable $Q$ and then partitioning this $Q$ into independent $x$ and $z$ components and then consider multiples of $x,y,z$ by an odd number $U$

I don't know if this characterizes all solutions for $G > 0 $ but it is worth exploring the algorithm.

Now if $G = 0$

$$x + y + z - \frac{2xy}{x + y - z}$$

Needs to be odd. Note that since $x,z$ are odd integers and $y$ is even it follows that:

$$\frac{2xy}{x + y - z}$$

Must be odd which implies that (after decomposing y)

$$\frac{2^{r+1}xL}{x - z + 2^{r}L}$$

Must be odd given odd numbers x,L,z. Again an algorithm has been generated. Selected a value y, from this y compute the decomposition, from which to select a Q such that $Q + y = 2^{r+1}$ and then decompose Q into the difference of 2 odd numbers $x,z$ such that $x,z,L$ do not share common factors.

Curiously this process is exactly the same thing as the previous process.