72

The complex power series $$\sum_{n=1}^{\infty}\frac{z^{n^2}}{n^2}$$ has radius $1$ (Ratio Test) and is absolutely convergent along $|z|=1$. Recalling something that my calculus professor (Ray Mayer, emeritus of Reed College) showed me 15 years ago, I started looking at a "graph" of this function. More precisely, here are plots of the images of $z$ with constant magnitude under this power series.

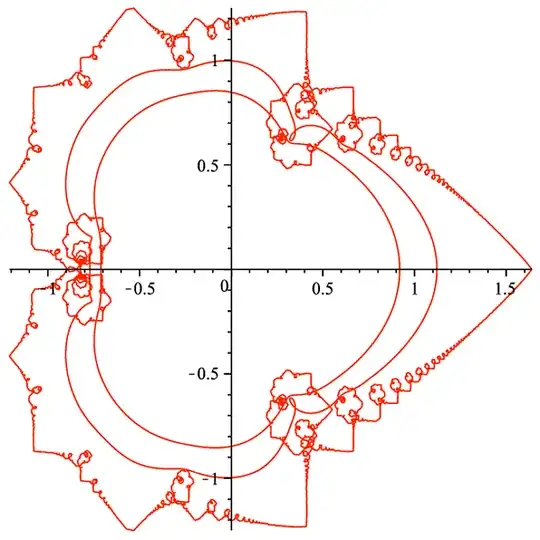
graph of the fractal

(The mapped curves are the images of $|z|=1$, $|z|=0.9$, and $|z|=0.8$. At the far right you can see $\sum\limits_{n=1}^{\infty}\frac1{n^2}=\frac{\pi^2}{6}$.)

So... what the heck is going on with the fractal behavior of the image of the boundary? Is there any understanding of this kind of behavior from power series? For instance, rotating $z$ by some angles might leave you with roughly the original series after a bit of rotation, scaling and translation. But I haven't been able to see how that would all come together.

I have a hunch that the "berries" along the inside of the leaf happen around values of $z$ with interesting arguments, but I haven't sat down to map out what those arguments might be.

EDIT: Indeed, the "leaftips" and "berries" seem to happen at regular $z$ values. Starting at the largest leaftip in quadrant I and moving clockwise, the leaftips are the images of $\exp\left(\frac{\pi}{2}i\right), \exp\left(\frac{\pi}{4}i\right), \exp\left(\frac{\pi}{6}i\right)$,... Similarly, starting from the largest berry and moving clockwise the "seeds" of the berries are the images of $\exp\left(\frac{\pi}{3}i\right), \exp\left(\frac{\pi}{5}i\right), \exp\left(\frac{\pi}{7}i\right)$,...

It appears that the "arc" from the large berry in quadrant IV to the large berry in quadrant I is parametrized by $\exp(it)$ with $t\in\left(-\frac{\pi}{3},\frac{\pi}{3}\right)$. Further, that the large leaf in quadrant I that crosses into quadrant II is parametrized by $t\in\left(\frac{3\pi}{7},\frac{3\pi}{5}\right)$. These two sections (and indeed any of the "leaves", "subleaves", etc.) ought to be similar in the fractal sense.

J. M. ain't a mathematician
  • 76,540
2'5 9'2
  • 56,991
  • 5
    I should note that this is just one example. This behavior is showing up for similar graphs of $\sum_{n=n_0}^{\infty}\frac{z^{f(n)}}{f(n)}$, where $f$ is other increasing functions from $\mathbb{N}$ to $\mathbb{N}$. So far, this one and the one with $f(n)=\binom{2n}{n}$ are my favorites. – 2'5 9'2 Nov 23 '11 at 00:38
  • Very intriguing! A random observation: your series is an antiderivative of $\sum_n z^{f(n)-1}$, an (almost) lacunary series. This sort of suggests trying to replace the "nice" $f(n)$ by $f(n)+1$. Also: what happens if you integrate once more? – hmakholm left over Monica Nov 23 '11 at 01:07
  • How do you compute the series? – lhf Nov 23 '11 at 01:14
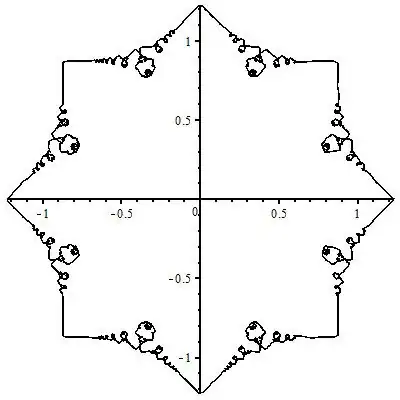
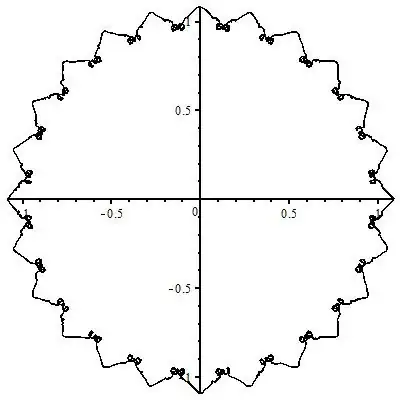
  • @lhf By approximation - just summing over the first $N$ terms. Although I think that smaller choices for N and m would still give smooth pictures in shorter time, here are the Maple commands that I used: with(plots); m := 2000; N := 200; L := seq(evalf(sum(exp(I*n^2*t)/n^2, n = 1 .. N)), t = 0 .. 3.1415926, 3.1415926/m): display(complexplot([L]), complexplot(map(conjugate, [L]))); – 2'5 9'2 Nov 23 '11 at 01:29
  • @Henning That's interesting - I wonder if experts on lacunary series would have anything to say about this then. I tried plotting antiderivatives in a few cases, and they don't exhibit the same fractal behavior. In hindsight that makes sense, since these functions are locally close enough to constant that their antiderivatives would be locally close to linear. – 2'5 9'2 Nov 23 '11 at 01:37
  • @Henning: And summing $\frac{z^{n^2+1}}{n^2+1}$ still produces fractal behavior. If the graph above has a maple leaf shape and wraps once around the origin, I'd say the graph for $f(n)=n^2+1$ has more of an arrowhead shape and it wraps around twice. – 2'5 9'2 Nov 23 '11 at 01:46
  • If you separate out real and imaginary parts, note that the components look awfully like those canonical "continuous-but-nowhere-differentiable" functions, like Riemann's or Weierstrass's... – J. M. ain't a mathematician Nov 23 '11 at 03:23
  • 4
    ...and speaking of which, the imaginary part of your sum essentially already is Weierstrass's function. – J. M. ain't a mathematician Nov 23 '11 at 03:38
  • BTW, you might want to see this paper. – J. M. ain't a mathematician Nov 23 '11 at 06:39
  • In case my comments have been too obtuse: the fractal behavior observed in your curves is already apparent in the Weierstrass nowhere-differentiable function; it stands to reason that your curves will inherit that behavior. – J. M. ain't a mathematician Dec 05 '11 at 09:56
  • alex.jordan: I suggest you erase the first term of the series, i.e z, and then instead of the all the series use the 2 nd and 3 rd terms. Do as you did above. You will get pointwise sum o two small circles with different radii, but "pointwise" sum will be according to actions of z^2 and z^9 on the circle. – niyazi Dec 05 '11 at 13:30
  • I meant z^4. If you add z and increase the number of terms used in the approximation of the series, you will get a bigger and better approximation to the above fractal. – niyazi Dec 05 '11 at 13:36
  • 1
    @J.M. I agree that the known information about Weierstrauss's function will almost certainly help (if not fully) explain this image. In another week I might finally have time to read up on it and I might ask you to link that article as an answer. But I'm also interested in the similar fractal behavior that I see for any $\sum \frac{x^{f(n)}}{f(n)}$ where $f$ grows fast enough for the series to be absolutely convergent when $|x|=1$. $\sum \frac{x^{n!}}{n!}$, $\sum \frac{x^{\binom{2n}{n}}}{\binom{2n}{n}}$, and $\sum \frac{x^{2^n}}{2^n}$ are some examples. – 2'5 9'2 Dec 05 '11 at 17:12
  • 1
    Note that to get the Weierstrass function you actually want to use $f(n)=b^n$ (maybe with a factor of $\pi$). In your base example, with $f(n)=n^2$, you actually get Riemann's "nowhere" differentiable function $$R(\theta)=\sum_{n\ge 0} {\sin\big(n^2\theta\big)\over n^2}$$ This is actually differentiable at points of the form $\pi{2p+1\over 2q+1}$, where $p$ and $q$ are integers. I'm not sure what goes on for other $f(n)$ (e.g. $f(n)=n^{k}$ for $k>2$), though $f(n)=n!$ nearly gives Darboux's function. See this paper for references: http://epubl.ltu.se/1402-1617/2003/320/LTU-EX-03320-SE.pdf – B R Dec 08 '11 at 19:57
  • If anyone would like to summarize what has been said in the comments, I'll gladly award the bounty to them. – Bruno Joyal Dec 09 '11 at 21:11
  • Some putzing around with the search terms "lacunary Fourier series" fractal turned up a few... interesting results. – J. M. ain't a mathematician Dec 10 '11 at 00:47
  • 1
    $f(n)=n$ is actually also... exciting. – Raskolnikov Dec 10 '11 at 12:18
  • 1
    It gets even more funny when you take different functions $f(n)$ and $g(n)$ for the powers and the factors resp., i.e. $\sum_{n=1}z^{f(n)}/g(n)$. – Raskolnikov Dec 10 '11 at 13:05
  • Take $f(n)=2.5\cdot 2^n+1$ and $g(n)=(1.62)^n$. – Raskolnikov Dec 10 '11 at 13:22
  • I wish to add the following: The derivative of $f(z)$ is the well-known theta function:(http://functions.wolfram.com/EllipticFunctions/EllipticTheta1/) – Kerry Dec 13 '11 at 02:24
  • A related question is now on MO – t.b. Dec 13 '11 at 07:06
  • 1
    A Google search gave me this... diagrams like the ones here http://www.uam.es/personal_pdi/ciencias/acordoba/documentos/articulos/DifferentiabilityandDimension.pdf , exact calculations here http://mathworld.wolfram.com/WeierstrassFunction.html . – GEdgar Dec 13 '11 at 13:24
  • This generates the graph:http://www.wolframalpha.com/input/?i=ParametricPlot%5B+%7B%5Csum%5E%7B500%7D_%7Bn%3D1%7D%5Cfrac%7Bcos%5Bn%5E%7B2%7Dx%5D%7D%7Bn%5E%7B2%7D%7D%2C%5Csum%5E%7B500%7D_%7Bn%3D1%7D%5Cfrac%7BSin%5Bn%5E%7B2%7Dx%5D%7D%7Bn%5E%7B2%7D%7D%7D%2C%7Bx%2C0%2C2%5Cpi%7D%5D – Kerry Dec 14 '11 at 04:58
  • I'm not sure I'm adding anything here, but there is a result - the Hadamard Gap theorem: http://en.wikipedia.org/wiki/Ostrowski%E2%80%93Hadamard_gap_theorem - that if the powers in a power series grow sufficiently quickly, the series is lacunary. One would then expect some sort of highly nondifferentiable behavior on the boundary of the disc of convergence, because otherwise what's the obstruction to analytic continuation? So perhaps it's not so surprising that we get these crazy fractals for a wide class of power series where the powers grow fast? – Ben Blum-Smith Dec 22 '11 at 04:12

1 Answers1

15

Let $f(z) = \sum_{n=1}^\infty \frac{z^{n^2}}{n^2}$. Separate this into the parts with odd $n$ and even $n$: $f_o(z) = \sum_{n \text{ odd}} \frac{z^{n^2}}{n^2}$, $f_e(z) = \sum_{n \text{ even}} \frac{z^{n^2}}{n^2} = f(z^4)/4$. Thus $$f(z) = \sum_{j=0}^\infty f_o(z^{4^j})/4^j = f_o(z) + \frac{f_o(z^4)}{4} + \frac{f_o(z^{16})}{16} + \ldots$$ The plot of $f_o(e^{it})$ for $0 \le t \le 2 \pi$ looks like this:

enter image description here

To produce the plot of $f(e^{it})$, think of a point going around the plot of $f_o$, and then a second describing a similar motion around that point but with 4 times the speed and 1/4 the scale, a third going around the second with $4^2$ times the speed and $1/4^2$ the scale of the original, etc.

The symmetry of the graph of $f_o$ is due to the fact that $f_o(e^{i\pi/4} z) = e^{i\pi/4} f_o(z)$ as well as $f_o(\overline{z}) = \overline{f_o(z)}$.

$f_o$ itself can be separated into parts for $n \equiv 0 \mod 3$ and $n \equiv 1 \text{ or } 2 \mod 3$: if $g = \sum_{n \equiv 1 \text{ or } 5 \mod 6} z^{n^2}/{n^2}$, we have $$f_o(z) = \sum_{j=0}^\infty g(z^{9^j})/9^j = g(z) + \frac{g(z^9)}{9} + \frac{g(z^{81})}{81} + \ldots $$

The plot of $g(e^{it})$ looks like this:

enter image description here

with symmetry coming from the fact that $g(e^{i\pi/12} z) = e^{i\pi/12} g(z)$.

Robert Israel
  • 470,583
  • 3
    Hi Robert - I think this is an excellent breakdown of the major (non-fractal) symmetry down to the function you have dubbed $g$. But have you suggested an explanation for the fractal symmetry? For instance, are you suggesting that this breakdown continues to arbitrarily high degree? And a totally different question: could this "break-down" approach apply to general $\sum\frac{z^{f(n)}}{f(n)}$? – 2'5 9'2 Dec 22 '11 at 02:58
  • 2
    It has to do with the fractal almost-symmetry too. $f(z) = f_o(z) + f(z^4)/4$. So whatever happens at $z= e^{i\theta}$ is echoed, at $1/4$ the scale, at $z = e^{i\theta/4}$, $e^{i(\theta/4+\pi/2)}$, $e^{i(\theta/4 + \pi)}$, and $e^{i(\theta/4 + 3\pi/2)}$. – Robert Israel Dec 22 '11 at 04:08
  • Couldn't the same thing be said about functions not exhibiting fractal behavior? For instance, $\ln(z)=\ln(z^4)/4$ (for restricted values of $z$) , but along $|z|=1$, I don't believe $\ln$ has any fractal symmetry. So you are relying on the fractal symmetry inherent in your function $f_o$ to "echo" down to smaller scales. $f_o$ in turn seems to get its fractal symmetry from $g$. Can $g$'s fractal symmetry be explained? – 2'5 9'2 Dec 22 '11 at 05:42
  • Do you still consider this an answer to the question? I feel that all you have done is passed the buck. You've related the fractal symmetry of $f$ down to the fractal symmetry of $g$, and also explained the $24$-symmetry of $g$. But unless $g$ itself has fractal symmetry, it is not clear to me why the relation between $g$ and $f$ should give $f$ fractal symmetry. After all, the similar relationship between $\ln(z)$ and $\ln(z^k)/k$ does not give $\ln(z)$ fractal symmetry. – 2'5 9'2 Jan 02 '12 at 06:18