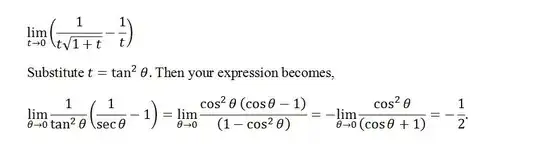Help solving a limit in two parts $\lim_{t\to 0}\left(\frac{1}{t\sqrt{1+t}}-\frac{1}{t}\right)$

Question

I'm trying to solve a limit problem but I've never encountered the one like this before.

$$ \lim_{t\to 0}\left(\frac{1}{t\sqrt{1+t}}-\frac{1}{t}\right)$$

I multiply the right side by $\frac{t\sqrt{1+t}}{t\sqrt{1+t}}$ and combine the terms to get:

$$ \lim_{t\to 0}\left(\frac{1 - t\sqrt{1+t}}{t\sqrt{1+t}}\right)$$

I can factor out the $t\sqrt{1+t}$ and I am left with:

$$1 - 1 = 0$$

This seems wrong to me. I can't explain why, maybe I just feel that getting a zero after all that work seems lame. Am I following the right steps?

Answer 1

$$\lim_{t\to 0}\left(\frac{1}{t\sqrt{1+t}}-\frac{1}{t}\right)=\lim_{t\to 0}\left[\frac{1}{t}\left(\frac{1}{\sqrt{1+t}}-1\right)\right]=\lim_{t\to 0}\left[\frac{1}{t}\left(\frac{1-\sqrt{1+t}}{\sqrt{1+t}}\right)\right]=\lim_{t\to 0}\left[\frac{1}{t}\left(\frac{1-\sqrt{1+t}}{\sqrt{1+t}}\right)\frac{1+\sqrt{1+t}}{1+\sqrt{1+t}}\right]=\lim_{t\to 0}\left[\frac{1}{t}\left(\frac{1-{1-t}}{\sqrt{1+t}}\right)\frac{1}{1+\sqrt{1+t}}\right]=\lim_{t \to 0}\frac{-1}{\sqrt{1+t}(1+\sqrt{1+t})}=\frac{-1}{2}$$

Answer 2

Using L'Hopital's rule,

$$\begin{align} \lim_{t\to 0}\left(\frac{1}{t\sqrt{1+t}}-\frac{1}{t}\right)&=\lim_{t\to 0}\frac{\frac{1}{\sqrt{1+t}}-1}{t}\\ &=\lim_{t\to 0}\frac{\frac{d}{dt}\left(\frac{1}{\sqrt{1+t}}-1\right)}{\frac{d}{dt}\left(t\right)}\\ &=\lim_{t\to 0}\frac{-1}{2(t+1)^{3/2}}\\ &=-\frac12. \end{align}$$

Answer 3

Apply L' Hospital rule . . The answer is $- \frac{1}{2}$

Answer 4

If you learnt Taylor series, the problem can be adddressed in a very simple form since, built around $t=0$, $$\frac{1}{\sqrt{1+t}}=1-\frac{t}{2}+O\left(t^2\right)$$ from which the remaining becomes very simple.

Answer 5

Let me show you a solution that computes the right limit $t\to 0^+$

Answer 6

Once you corrected your second formula to $$ \begin{align} \lim_{t\to0}\left(\frac1{t\sqrt{1+t}}-\frac1t\right) &=\lim_{t\to0}\frac{1-\sqrt{1+t}}{t\sqrt{1+t}}\\ &=\lim_{t\to0}\frac{1-\sqrt{1+t}}{t}\ \lim_{t\to0}\frac1{\sqrt{1+t}} \end{align} $$ You can use L'Hospital on the left limit and just plug $t=0$ into the right limit.