complex equations question

Question

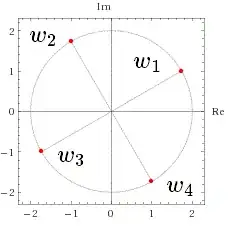
find all solutions of the equation: $w^4 = -8(1-i\sqrt{3})$

I dont wanna be that guy, but can someone tell me what the second solution to this equation is? cuz the solution manual says it's $-1 + i\sqrt{3}$ but I managed to get $1+i\sqrt{3}$, I managed to get the first solution right tho, on polar form this thing equation is $16\left(\cos\left(\frac{2\pi}{3}\right) + i\sin\left(\frac{2\pi}{3}\right)\right)$ which is $2(\cos\left(\frac{1}{4}\frac{2\pi}{3}\right) + i\sin\left(\frac{1}{4}\frac{2\pi}{3}\right)$ since $n = 4$ :P? note: the solution agrees completely with $2(\cos\left(\frac{1}{4}\frac{2\pi}{3}\right) + i\sin\left(\frac{1}{4}\frac{2\pi}{3}\right)$ so idk why im not able to find the second solution?

There is no 'first', 'second', ... solutions. For a way to solve this, see the first part of this answer. — Git Gud, Jun 15 '14 at 21:23
ok I managed to find when k=0 but not when k=1, can you help me now? :P — yyzzer1234, Jun 15 '14 at 21:25

beep-boop · Accepted Answer · 2014-06-15T22:10:05.920

2

Right, we've got $w^4=-8[1-i\sqrt{3}]=-8+8\sqrt{3}i$.

Let's convert this into polar form (which I'll leave as an exercise for you), giving: $$w^4=16e^{i\frac{2\pi}{3}}=\underbrace{16e^{i\left(\frac{2\pi}{3}+2k\pi\right)}}_{\textrm{adding a multiple of 2} \pi \ \textrm{makes no difference to the argument}}.$$

Take the fourth roots of both sides, to give: $$w=2e^{i\left(\frac{\pi}{6}+k \frac{\pi}{2} \right)}$$ for $k \in \mathbb{Z}$.

Now just sub in $k=1,2,3,4$ (or any four consecutive integers) and you're done.

P.S. You might want to convert polar form into rectangular form using the identity $e^{i\theta}\equiv\cos(\theta)+i\sin(\theta)$.

P.P.S. There seems to be a bit of (understandable) confusion about the order of the complex roots. Generally, we take the first root to be the one with the smallest argument (starting from the positive real axis, and going anticlockwise), but it really doesn't matter.

Here are all four roots on an Argand diagram:

enter image description here

edited Jun 15 '14 at 22:10

answered Jun 15 '14 at 21:46

beep-boop

11,825

Well, let's find one root together. Let $k=0$ (say).
Then $w_1=2e^{(i \pi/6)}=2[\cos(\pi /6)+i\sin(\pi/6)]=2[\frac{\sqrt{3}}{2}+0.5i]=\sqrt{3}+i$.

To find the other 3 roots, sub in $k=1, k=2, k=3$ into $2e^{i(\pi/6+k\pi)}$.
– beep-boop Jun 15 '14 at 21:53
@yyzzer1234 It doesn't matter. $k$ could be $301$ as long as it's an integer. After every four integers, the solution repeats itself. – beep-boop Jun 15 '14 at 21:58
Plug $k=2$ into the formula. – beep-boop Jun 15 '14 at 21:59
Yep- but $\frac{2k\pi}{n}=\frac{2k\pi}{4}=k\pi/2$. – beep-boop Jun 15 '14 at 22:05
Yep- sorry about that. Mistake corrected. – beep-boop Jun 15 '14 at 22:10

complex equations question

1 Answers1