0

The elliptic integral of the first kind $$ \int_0^{\pi/2}{\frac{du}{\sqrt{1-k^2\sin^2{u}}}} $$ cannot be expressed in terms of standard functions. But in the following context from The Pendulum by Baker the author says

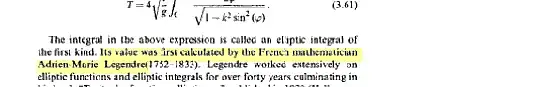
A part of the Pendulum by Baker

What is the meaning of the Its value in the above context? Can the elliptic integral be expressed in terms of standard functions?

J. M. ain't a mathematician
  • 76,540
Dante
  • 1,974
  • 1
    No, they probably just mean that it's form was first found then or some numerical computations were performed. – ClassicStyle Jun 08 '14 at 21:07
  • We just know so much integral-shaped identities about Elliptic Integrals. For this case, it's also interpreted as $\int_0^1\frac{\mathrm{d}x}{\sqrt{(1-x^2)(1-k^2x^2)}}$ which is similar to Christoffel Integrals which map Complex Upper Half Plane to polygens: http://math.stackexchange.com/questions/813698/an-identity-of-an-elliptical-integral – Fardad Pouran Jun 08 '14 at 21:15

0 Answers0