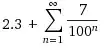2

I'm studying for a test and I have a question on the following problem.

Convert the repeating decimal $2.307070707\ldots$ into a fraction using geometric series.

I'm not sure if this is right, but this is what I did:
img

Did I get it right, or am I missing something? If it's wrong, what should I do?

Klangen
  • 5,459
Max G
  • 23
  • Duplicate of http://math.stackexchange.com/questions/793967/converting-repeating-decimal-numbers-to-fractions. – lhf Jun 03 '14 at 02:21
  • 1
    @lhf: not exactly a dupe, is it? That's a more general question, this is a specific one. – Deepak Jun 03 '14 at 02:29

2 Answers2

3

It's almost right; since the very first of the repeating $7$'s happens $3$ places down, you should actually have

$$2.3 + \frac{1}{10} \sum_{n = 1}^{\infty} \frac{7}{100^n}$$

(since each factor of $100$ moves the number two places to the right. Now since you want to find a fraction, you should evaluate the series:

$$= 2.3 + \frac{7}{1000} \sum_{n = 0}^{\infty} \frac{1}{100^n} = 2.3 + \frac{7}{1000} \frac{1}{1 - \frac{1}{100}}$$

which can obviously be simplified.

For a more direct way to proceed, notice that if $s$ is the given number, we have that

$$100 s - s= 230.70707... - 2.3070707... = 228.4$$

2

You have the basic idea but you need to "offset" the sequence by multiplying it by $\frac{1}{10}$.

$\displaystyle 2.3070707... = 2.3 + 0.0070707... = 2.3 + \frac{1}{10}(0.070707...) = 2.3 + \frac{1}{10}\sum_{n=1}^{\infty}\frac{7}{100^n} \\ \displaystyle = 2.3 + \frac{7}{10}\sum_{n=1}^{\infty}\frac{1}{100^n} = \frac{23}{10} + \frac{7}{10}\left( \frac{\frac{1}{100}}{1 - \frac{1}{100}}\right)\\ \displaystyle = \frac{23}{10} + \frac{7}{990} = \frac{2284}{990}\\ \displaystyle = \frac{1142}{495} $

Deepak
  • 27,479