9

The function $g:[0,1]\to[0,1]$ is continuously differentiable and increasing. Also, $g(0)=0$ and $g(1)=1$. Continuity and differentiability of higher orders can be assumed if necessary. The proposition on hand is the following:

If for all integers $t>0$ and for all $r\in(0,1)$, $g(r^{t+1})>g(r)\cdot g(r^t)$, then for all $p,q\in(0,1)$, $g(pq)\geq g(p)g(q)$.

Juanito
  • 2,482
  • 12
  • 25
  • 2
    It seems to me that you need to approximate $\ln p/\ln q$ well enough by a rational number $m/n$. Then use $r=q^{1/n}$, so $r^n=q$, and $r^m$ is close to $p$ as you want. You can easily prove by induction that the given condition implies $g(r^{m+n})>g(r^m)g(r^n)$. Letting the approximation improve in the limit you get at least $g(pq)\ge g(p)g(q)$. May be another idea is needed to get the strict inequality? – Jyrki Lahtonen May 26 '14 at 18:51
  • Hello Jyrki, thanks for your reply. I like your idea of approximating lnp/lnq by a rational number m/n. But, I do not see how, induction would imply g(r^(m+n))>g(r^m)g(r^n).For example, g(r^(t+2))>g(r^(t+1))g(r)>g(r^t)[g(r)]^2, which does not help the induction hypothesis. Were you alluding to a different way of using induction? – Juanito May 26 '14 at 19:32
  • Ahh! May be I just made a mistake there :-) – Jyrki Lahtonen May 26 '14 at 19:46
  • In your overflow posting you did not include $g(0)=0$ and $g(1)=1$. Is this maintained? –  May 28 '14 at 17:09
  • Hello @AthanagorWurlitzer, thanks for pointing it out, I think I missed out the additional condition in the overflow posting. $g(0)=0$ and $g(1)=1$ should still be there. I will edit the overflow post. – Juanito May 28 '14 at 18:44
  • 1
    It is easier to visualize if you write it instead $h(0)=1$, $\lim_{x\to\infty}h(x)=0$, and $$h((n+1)x)>h(x)+h(nx)$$ for all $x>0$. Your question is then does it imply $$h(x+y)>h(x)+h(y).$$ –  May 29 '14 at 12:00
  • @AthanagorWurlitzer In that case you should still use multiplication outside $h$. – Bart Michels May 29 '14 at 15:34
  • @barto to go from this problem to the suggested one (and vice-versa) write $x=-ln(r)$ and $g=\exp(h)$. –  May 29 '14 at 18:09
  • @AthanagorWurlitzer: Doesn't your reformulation of the hypothesis lead to an immediate contradiction? You've somehow mixed up the change of variables. – John M May 30 '14 at 00:37
  • @JyrkiLahtonen: How does your induction work? How do you show $g(r^5) > g(r^2) g(r^3)$? – John M May 30 '14 at 00:39
  • Hey @JohnM, I think I can answer your question, but I cannot post a pdf shot on the conversation, so I am writing it down as a separate answer. – Juanito May 30 '14 at 01:27
  • @AthanagorWurlitzer I think once you make a change of variables to get a additive inequality, the signs reverses, so, you get the reverse inequality. Maybe this is the point JohnM is making? – Juanito May 30 '14 at 01:58
  • What is the source of this problem, please? – Gerry Myerson Jul 16 '14 at 07:22

1 Answers1

5

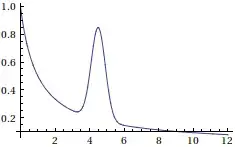
By setting $F(x)=-\log g(e^{-x})$ we get $F(0)=0,\lim_{x\to+\infty}F(x)=+\infty$ and: $$\forall x\in\mathbb{R}^+,\forall t\in\mathbb{N},\quad F((t+1)x)-F(tx)\leq F(x)-F(0),\tag{1}$$ that is a sort of concavity condition. $(1)$ can be re-written as: $$\forall x\in\mathbb{R}^+,\forall t\in\mathbb{N},\quad \int_{t}^{t+1} f(xt)\, dt \leq \int_{0}^{1}f(xt)\,dt.\tag{2}$$ It comes, almost by magic, that the function $$ f(x)=\frac{1}{x+1}+\frac{2}{3}\exp\left(-3(x-9/2)^2\right)$$ satisfies $(1)$ and the boundary conditions, however: $$ \int_{4}^{5}f(x)\,dx = 0.713993\ldots > 0.693147\ldots = \int_{0}^{1}f(x)\,dx, $$ so we just found a $C^\infty(\mathbb{R}^+)$ counter-example.

The graphics of $f(x)$

Jack D'Aurizio
  • 361,689
  • Do you mind me asking how you approached the problem? I would really like to learn. Also, given your complicated functional form, how did you check for all the possible inequalities the function needs to satisfy? – Juanito Jul 17 '14 at 17:57
  • 2
    I had a look at @doetoe's solution in http://math.stackexchange.com/questions/844013/additive-functional-inequality and try to found a regular function with the same characteristic; so I took $f(x)=\frac{1}{x+1}$ that suits the inequality nicely and introduced a gaussian perturbation by trial and error. – Jack D'Aurizio Jul 17 '14 at 18:02
  • 1
    I checked the inequality by the graphical way with the aid of Mathematica. It happens that since the perturbation is concentrated between $4$ and $5$, only the small values of $t$ (the ones below $6$) are really critical, for the remaining ones the separation between $F((t+1)x)-F(tx)$ and $F(x)$ is quite neat. – Jack D'Aurizio Jul 17 '14 at 18:07
  • Thanks for the reply. Could you tell me what it means to check an inequality in a graphical way? I am trying to learn. as I would like to be able to do something like this myself in the future. – Juanito Jul 17 '14 at 18:09
  • Just plot the graphics of the two functions and check that one is always above the other. It happens that for any value of $t$ the difference between $F((t+1)x)-F(tx)$ and $F(x)$ is large for large values of $x$ (this should be quite easy to prove "by hand"), hence the parameters choice can be completely computer-guided, in order to have a "machine proof". – Jack D'Aurizio Jul 17 '14 at 18:15
  • 1
    I understand what you are saying. Thanks for your patience. – Juanito Jul 17 '14 at 18:17