Why is the Koch curve homeomorphic to $[0,1]$?

Question

Henning Makholm has provided a nice proof that the limiting curve is a continuous function from $[0,1]$ to the plane. I was curios if the function is homeomorphism. A quick search gave me many sources mentioning that $[0,1]$ and the Koch curve are indeed homeomorphic (as a proof that they have the same topological dimension), yet without showing why are they homeomorphic. What would be the simplest way to show it?

Answer 1

The map from the interval onto the Koch curve is a continuous bijection from a compact space to a Hausdorff one. So it's closed since closed subsets of compact spaces are compact, images of compact spaces are compact, and compact subspaces of Hausdorff spaces are closed, and thus a homeomorphism.

To check this is indeed an injection from $I$ to its image, consider the following picture of one stage in the construction. Each point on some curve $\gamma_i$ is drawn directly above the point on $\gamma_{i+1}$ mapped to by the same point in $I$. One sees that only $D$ and $F$ are closer together on $\gamma_{i+1}$ than on $\gamma_i$. But even so they will never get closer than $3^{-i}$, the length of the segment containing just $E$-at the very least no closer than half this.

To see this, observe that only the tip of the new triangle lies directly above $F$'s segment, so that we can bound the distance between the whole segment $AE$ and the next triangle to the right, (out of frame,) by $3^{-i}$. And continuing the construction we can easily bound the image of $AE$ in the limit curve away from the out-of-frame triangle by $\frac{1}{2*3^{i}}$, since in later stages no point can move further than $\frac{1}{2*3^{i}}=\sum_k 3^{-i-1-k}$. Indeed at stage $j$ no point moves further than $\frac{\sqrt{3}}{2* 3^{j}}\leq 3^{-j}$.

So if $|\gamma_i(x)-\gamma_i(y)|>\delta$, then on the limit curve $|\gamma(x)-\gamma(y)|\geq \min(\delta,\frac{1}{2* 3^i})$, in particular, $\gamma(x)\neq \gamma(y)$ and $\gamma$ is injective.

Answer 2

Yes, the standard parameterization of the snowflake curve is injective.

To see this easily, instead of making each approximant a curve, we can make it a chain of linked half-open equilateral triangles:

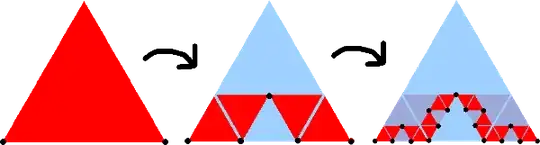
Each of the red triangles includes the side between the entry and exit point, but doesn't the two other sides. In each step each triangle splits into four smaller triangles that are completely contained in the original one. Therefore, at each step all of the small triangles are disjoint, except for the shared corner points where the curve moves from one triangle to the next (black dots in the diagram).

Now if we have a parameter value $x\in[0,1]$ and want to find $\gamma(x)$, write $x$ as a 4-ary fraction and then each digit will decide one of the 4 subtriangles to move into at each step in the construction. $\gamma(x)$ is then the unique point that is in the intersection of a sequence of smaller and smaller nested triangles.

If $x$ and $y$ are different parameter values, then their 4-ary expansions must differ from some point. But that means that $\gamma(x)$ and $\gamma(y)$ are in different small triangles at that step in the construction. Since the triangles don't have points in common, $\gamma(x)$ and $\gamma(y)$ are not the same point.

Answer 3

You can define the Koch curve without using a sequence of functions (I dislike sequences of functions)

First define $f$ on $[0,1] \cap \Bbb Z[1/2]$ (the dyadic rationals) inductively by :
$f(0)= (0,0)$, $f(1) = (1,0)$, and for $i=0 \ldots 3$, $f((x+i)/4) = T_i(f(x))$ where $T_0,T_1,T_2,T_3$ are the $4$ affine transformations
$T_0(x,y) =(\frac x 3,\frac y 3), \\ T_1(x,y) = (\frac 13+ \frac{x-\sqrt 3 y}6,\frac{\sqrt 3 x + y}6), \\ T_2(x,y) = (\frac 12+\frac{x+\sqrt 3 y}6, \frac{\sqrt 3}2 + \frac{-x+\sqrt 3 y}6), \\ T_3(x,y) = (\frac 23 + x,\frac y3)$

If $A^0$ is the triangle with vertices $(0,0),(1,0),(\frac 12,\frac{\sqrt 3}6)$, we can see that if $A^1_i = T_i(A^0)$ then $A^1_i \subset A^0$ ; any two $A^1_i,A^1_j$ have distinct interior ; two consecutives triangles are joined by a vertex ; the diameter of $A^1_i$ is $\frac 13$ the diameter of $A^0$.

The points $f(x)$ for $x$ a dyadic rational are vertices of the images of the initial triangle by the various iterations of the $4$ transformations (with usually two possibilities).

The facts that $T_{i+1}(0,0) = T_i(1,0)$ (two consecutive triangles are connected),and that the diameters of the triangles decrease exponentially prove that $f$ is uniformly continuous : if $|x-y| \le 1/4^n$ then $x$ and $y$ are either in the same triangle $A^n_k$ or in two consecutive triangles $A^n_k,A^n_{k+1}$, which shows that $d(f(x),f(y)) \le 2/3^n$.

The fact that the $4$ triangles $T^1_i$ are almost disjoint proves that $f$ is "uniformly injective". We can show with a few pictures that if you pick a triangle $T^n_k$ and remove its two neighbourhing triangles, the rest of the $T^n_{k'}$ triangles will be at a distance $\ge C/3^n$ for some $C > 0$. Therefore, if $|x-y| > 2/4^n$, then $d(f(x),f(y)) \ge C/3^n$.

Now we can extend the definition of $f$ on $[0;1]$ by continuity. It's easy to show that $f$ stays uniformly continuous and uniformly injective (hence it stays injective). So $f$ is a continuous bijection on its image. When you take the contrapositive of the uniform injectivity, you obtain that $f^{-1}$ is uniformly continuous, so that $f$ is a homeomorphism.