How can I find the solution for the following equation in $a,b \mbox{ and } c$.
$$\frac{a}{c-b+1}+\frac{b}{a-c+1}+\frac{c}{b-a+1}=0.$$ Also $b-c \neq 1$, $c-a \neq 1$ and $a-b \neq 1$.
Thanks!
Asked
Active
Viewed 445 times
7
-
What have you tried so far? A common method is to transform the expression into a single fraction: something over something else. Then it is sufficient to solve the top of the fraction for 0. – May 21 '14 at 06:34
-
With one equation you can't get absolute values for three constants , for instance you have a solution of $(a, b, c) = (0, 0, 0)$ but this is far from unique. The best you'll be able to do (without more equations) is give an expression (probably not linear) for $a$ in terms of $b$ and $c$. – Stijn Hanson May 21 '14 at 06:54
-
@Stijn: Not saying this is the case here, but for example $x^2 + y^2 = 0$ has only one solution over the reals. – J. J. May 21 '14 at 06:57
-
In fact it is not hard to see that Stijn is correct in this case: By doing what beanshadow suggested, the numerator will be a 3rd degree polynomial in $a$, and thus has a root for every choice of $b$ and $c$. – J. J. May 21 '14 at 06:59
-
Here's a start: making the equation into a single fraction yields $$\frac{a(a-c+1)(b-a+1)+b(c-b+1)(b-a+1)+c(c-b+1)(a-c+1)}{(c-b+1)(a-c+1)(b-a+1)}=0,$$ which holds if and only if the numerator equals $0$. Expanding the whole thing we find $$(a+b+c)+(a^2b+a^2c+ab^2+b^2c+ac^2+bc^2)-(a^3+b^3+c^3)-3abc=0,$$ which 'simplifies' to $$(a+b+c)+(a+b-c)(b+c-a)(c+a-b)-abc=0.$$ But I don't see any nice way to express the solutions $(a,b,c)$ of this thing. – Servaes May 21 '14 at 08:34
-
Are we looking for solutions in reals or in integers? – Peter Košinár Jun 04 '14 at 08:56
-
any kind of solutions. – Iuli Jun 04 '14 at 09:37
1 Answers
20
In order to avoid definiteness problems, I will consider $a$, $b$ and $c$ as independent variables in the field of rational fractions $\mathbb{C}(a,b,c)$, and I will seek some kind of a parametric representation of the solutions $(a,b,c)$ of the proposed equation as rational functions from $\mathbb{C}(u,v)$ where $u$ and $v$ are independent variables. Precisely, I will prove that $$ \frac{a}{c-b+1}+\frac{b}{a-c+1}+\frac{c}{b-a+1}=0, $$ If and only if $$\eqalign{ a&=\frac{u \left(3 u v+u+3 v^2+2 v-1\right)}{u^2+u v+v^2-1}\cr b&=\frac{v \left(3 u^2+3 u v-2 u-v-1\right)}{u^2+u v+v^2-1}\cr c&=\frac{(u+v) (3 u v-u+v+1)}{u^2+u v+v^2-1}\cr } $$ To see this, let $$u=\frac{a}{c-b+1}, v=\frac{b}{a-c+1},w=\frac{c}{b-a+1}.\tag{1}$$ The proposed equation is, then, equivalent to $w=-u-v$. Now $(1)$ is equivalent to $$ \left[\matrix{1&u&-u\cr-v&1&v\cr w&-w&1 }\right]\cdot\left[\matrix{a\cr b\cr c}\right]=\left[\matrix{u\cr v\cr w}\right] $$ or $$ \left[\matrix{a\cr b\cr c}\right]=\left[\matrix{1&u&-u\cr-v&1&v\cr w&-w&1 }\right]^{-1}\cdot\left[\matrix{u\cr v\cr w}\right] $$ This yields, after some algebra, $$\eqalign {a&=\frac{u (3 v w-v+w+1)}{u v+u w+v w+1}\cr b&=\frac{v (3 u w+u-w+1)}{u v+u w+v w+1}\cr c&=\frac{w (3 u v-u+v+1)}{u v+u w+v w+1} } $$ Now, the condition $w=-u-v$ yields (after substitution) the announced parametrization of the solutions.
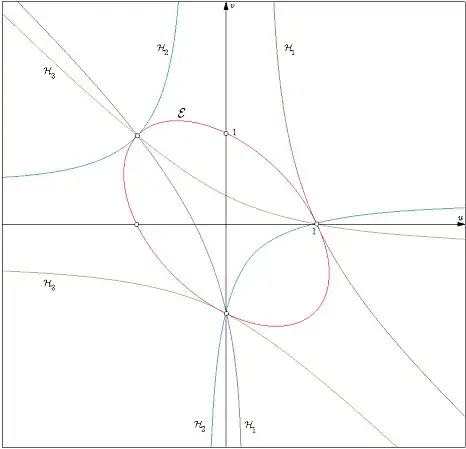
Edit. If we want to substitute $u$ and $v$ by real numbers then $$(u,v)\in\mathbb{R}\times\mathbb{R}\setminus\left(\mathcal{E}\cup\mathcal{H}_1\cup\mathcal{H}_2\cup\mathcal{H}_3\right)$$
where $\mathcal{E}$ is the ellipse of equation $u^2+uv+v^2=1$, and $\mathcal{H}_k$ ($k=1,2,3$) are the hyperbola corresponding to the conditions $a-c=1$ (or equivalently $3uv-v-2u+3u^2=1$), $b-a=1$ (or equivalently $3uv+v-u=-1$), and $c-b=1$ (or equivalently $3uv+u+2v+3v^2=1$).
$$
\eqalign{\mathcal{E}:& \quad u^2+uv+v^2=1\cr
\mathcal{H}_1:& \quad 3uv-v-2u+3u^2=1\cr
\mathcal{H}_2:& \quad 3uv+v-u=-1\cr
\mathcal{H}_3:& \quad 3uv+u+2v+3v^2=1
}$$
The next figure depicts this set:
Omran Kouba
- 29,112
-
Nitpicking: with exception of the (rotated) ellipse that makes the denominator zero i.e. $$ \frac{(u+v)^2}{(2/\sqrt{3})^2}+\frac{(u-v)^2}{2^2}=1 $$ – Han de Bruijn Jun 05 '14 at 13:40
-
@HandeBruijn, Here $u,v$ are independent variables in the field of fractions $\mathbb{C}(u,v)$. If we want to substitute $u$ and $v$ with numbers we have to suppose that denominators do not vanish, and that $b-c\ne1$,...etc. This yields several conditions, one of them is your exception. – Omran Kouba Jun 05 '14 at 17:15
-
The other conditions are $u+2v+3v^2+3vu \ne 1$ , $3vu-v+3u^2-2u \ne 1$ , $-(v+3vu-u) \ne 1$ . But I suppose these exceptions are not necessary if the solutions are restricted to "the field of fractions", as you say. Is that right ? (Note: as a physicist by education, I'm not used to distinguish much between real and rational numbers) – Han de Bruijn Jun 06 '14 at 11:52
-
@HandeBruijn, Yes, you are right. The "field of fractions in two variables $\mathbb{C}(u,v)$" is the field of all expressions of the form $P(u,v)/Q(u,v)$ where $P$ and $Q$ are complex polynomials in the variables $u$ and $v$. We distinguish between a polynomial $P(X)=a_0+\cdots+a_nX^n$ as a 'symbolic expression' and the associated function $x\mapsto P(x)$. This distinction is most important, and necessary, when underlying field of the coefficient has characteristic different from $0$. – Omran Kouba Jun 06 '14 at 16:55
-
-
-