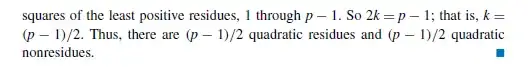Help needed in understanding proof: Every odd prime $p$ has exactly $(p-1)/2$ quadratic residues and $(p-1)/2$ quadratic nonresidues.

Question

Help needed in understanding proof: Every odd prime $p$ has exactly $(p-1)/2$ quadratic residues and $(p-1)/2$ quadratic nonresidues.

We assume there exist $k$ incongruent quadratic residues and each yield two solutions of the equation $x^2 \equiv a (\mod p)$. Also each of these solutions are incongruent, right ? So we have $2k$ solutions to quadratic congruences.

Then there are $p-1$ squares of the least residues, $1$ through $p-1$. But these need not be incongruent (consider $p = 7$ and $1^2, 6^2$). Then $2k = p-1$, why ?

Could someone explain to me in details what the reasoning is ?

Answer 1

If a nonzero number $y$ is a square modulo $p>2$, say $=x^2$, then it is also $=(-x)^2$. But $x=-x=\mod p\iff p\mid 2x\iff p\mid x$ since $p$ is odd, so these numbers are distinct. Moreover, since $\Bbb Z_p$ is a field, $x^2=y$ has at most two solutions, hence none or exactly two by the above. It follows that if $k$ is the number of quadratic residues, there are $2k$ noncongruent elements in $\Bbb Z_p$. Thus, $k\leqslant \dfrac{p-1}2$.

Consider now the $p-1$ numbers $1,2,\ldots,\frac{p-1}2,-\frac{p-1}2,\ldots,-2,-1$. These are all the nonzero classes modulo $p$, and squaring them gives $\frac{p-1}2$ squares. Thus $k\geqslant \dfrac{p-1}2$.

Answer 2

Alternatively, if $x^{2} \equiv y^{2}$ (mod $p$), then $(x-y)(x+y) \equiv 0$ (mod $p$). Since $p$ is prime, this gives $x \equiv \pm y$ (mod $p$). Hence $1^{2},2^{2}, \ldots, \left(\frac{p-1}{2}\right)^{2}$ are all incongruent (mod $p$) and for $\frac{p+1}{2} \leq x \leq p-1,$ we see that $x^{2} \equiv (p-x)^{2}$ (mod $p$) so is congruent to one and only one of $1^{2},2^{2}, \ldots, \left(\frac{p-1}{2}\right)^{2}$ (mod $p$).

Answer 3

The simplest proof uses a bit of group theory.

Consider the map $x \mapsto x^2$ in $U_p=(\mathbb Z/p\mathbb Z)^{\times}$. This is a group homomorphism.

The kernel of the map has order $2$ because $x^2=1$ iff $p \mid (x-1)(x+1)$ iff $x\equiv \pm 1 \bmod p$.

Hence the image has order $(p-1)/2$. Of course, the image is the set of quadratic residues.

The argument above is just a sophisticated way of counting preimages, as in Pedro's argument. Essentially it says that every value in the image has exactly two preimages and so there are $(p-1)/2$ values in the image.