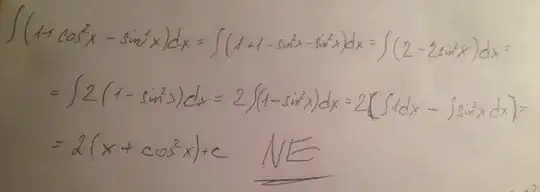1

I am solving this example:

enter image description here

Transcription:

\begin{align} &\int(1+\cos^2x-\sin^2x)dx=\int(1+1-\sin^2x-\sin^2x)dx=\int(2-2\sin^2x)dx=\\ &\quad=\int2(1-\sin^2x)dx=2\int(1-\sin^2x)dx=2\left[\int1dx-\int\sin^2xdx\right]=\\ &\quad=2(x+\cos^2x)+c \end{align}

But I am still wrong -- cannot find the right result. Could you help me, please, what am I doing wrong?

Thanks

Martin Sleziak
  • 56,060
user984621
  • 331

3 Answers3

2

Here's a different route for finding the anti-derivative that doesn't rely on any trigonometric identities at all, save the derivatives of sine and cosine. Simple algebraic manipulation gives $$\int(\cos^2{x}-\sin^2{x})dx=\int(\cos{x}+\sin{x})(\cos{x}-\sin{x})dx.$$

Note that the derivative of $\cos{x}+\sin{x}$ is $\frac{d}{dx}(\sin{x}+\cos{x})=\cos{x}-\sin{x}$, which prompts the substitution $u=\cos{x}+\sin{x}$ in the integral above. Then,

$$\int(\cos^2{x}-\sin^2{x})dx=\int(\cos{x}+\sin{x})(\cos{x}-\sin{x})dx\\ =\int u\,du\\ =\frac12u^2+constant\\ =\frac12(\cos{x}+\sin{x})^2+constant$$

It follows immediately that the integral considered in your question is

$$\int(1+\cos^2{x}-\sin^2{x})dx=x+\frac12(\cos{x}+\sin{x})^2+constant.$$

Appendix: One might wish to verify the anti-derivative $F(x)=x+\frac12(\cos{x}+\sin{x})^2$ found by the method in this answer is consistent with the anti-derivative $G(x)=x+\frac12\sin{(2x)}$ arrived at in responses by other users. If you're suspicious that $F(x)\neq G(x)$, you'd be right. Beginners sometimes get tripped up by this, because they forget anti-derivatives need not be equal (all those times your high-school calculus teacher nagged on you to remember that pesky "+ constant", she really wasn't just being an insufferable pedant!). Indeed,

$$(\cos{x}+\sin{x})^2=\cos^2{x}+\sin^2{x}+2\cos{x}\sin{x}=1+\sin{(2x)}\\ \implies \frac12(\cos{x}+\sin{x})^2 - \frac12\sin{(2x)} = \frac12.$$

Since $F$ and $G$ only differ by a constant, they are consistent.

David H
  • 32,536
  • 1
    Nice. It reminded me this solution: http://math.stackexchange.com/questions/180744/compute-int-frac-sinx-sinx-cosx-mathrm-dx/180746#180746 – Martin Sleziak May 03 '14 at 14:04
  • @MartinSleziak Oh wow. 'Slick' doesn't even begin to describe that method of solution. Thanks a bunch for sharing. – David H May 03 '14 at 14:16
1

It is wrong because $\int \sin^2(x)dx$ $\neq $$-\cos^2(x)+c$.

For this integral use the double angle trigonometric formulas:

$\sin^2(x)=\frac{{1-\cos(2x)}}{2}$

or

$\cos^2(x)=\frac{{1+\cos(2x)}}{2}$. Therefore if we call the integral $I$, then

$I=2\int \cos^2(x)dx=\int (1+cos(2x))dx=x+1/2\sin(2x)+c.$

Martin Sleziak
  • 56,060
Fermat
  • 5,366
  • Hamid, thank you for your message, the result is correct. However, I still don't know how to count it - could you, please, outline it a bit more in detail? – user984621 May 02 '14 at 21:45
  • look at the last term of the second line of your uploaded picture. It is $2\int \cos^2(x)dx$. But $2\int \frac{1}{2}dx=2\frac{x}{2}=x$and $\int \cos(2x)dx=\frac{1}{2}\sin(2x)$. please mark the answer as acceptable if it helps you. – Fermat May 03 '14 at 13:00
1

Recall that $\cos^2 x - \sin^2 x = \cos 2x$.

Then we have $\displaystyle \int [1 + \cos (2x)] dx = x + \frac{1}{2} \sin (2x) + C$

MT_
  • 19,971