Since my old answer has gotten 2 downvotes, and the comments explain pretty much what people found objectionable about my presentation, I have rewritten it, hopefully to present my ideas in a more acceptable fashion. I have separated my answer into two sections; one for a real analysis approach, and another for a complex analysis approach.
Real Analysis
When $y\gt3$, we have $\frac{\mathrm{d}}{\mathrm{d}y}\log(y-3)=\frac1{y-3}$. Therefore, for $y\gt3$, we have
$$
\int\frac{\mathrm{d}y}{y-3}=\log(y-3)+C\tag{1}
$$
When $y\lt3$, we have $\frac{\mathrm{d}}{\mathrm{d}y}\log(3-y)=\frac1{y-3}$. Therefore, for $y\lt3$, we have
$$
\int\frac{\mathrm{d}y}{y-3}=\log(3-y)+C\tag{2}
$$
For convenience, we can combine $(1)$ and $(2)$ into
$$
\int\frac{\mathrm{d}y}{y-3}=\log|y-3|+C\tag{3}
$$
However, $(3)$ must be handled with a bit of care: it cannot be applied to a definite integral with limits on both sides of $3$. For example,
$$
\int_2^4\frac{\mathrm{d}y}{y-3}\tag{4}
$$
does not converge. This is because neither
$$
\int_2^3\frac{\mathrm{d}y}{y-3}\qquad\text{nor}\qquad\int_3^4\frac{\mathrm{d}y}{y-3}\tag{5}
$$
converge. However, $(4)$ has a Cauchy Principal Value of $0$.
Complex Analysis
As a function on $\mathbb{C}$, $\log|y-3|$ is not differentiable. Therefore, while $(1)$ and $(2)$ still hold, unfortunately, $(3)$, the convenience form for paths in $\mathbb{R}\!\setminus\!\{3\}$, does not.
When restricted to $\mathbb{R}$, any path from $2$ to $4$ must pass through $3$ and we run into the problems presented in $(4)$ and $(5)$. However, in $\mathbb{C}$, there are many paths from $2$ to $4$ that do not pass through $3$. For example, the path $\gamma_1:[0,1]\to\mathbb{C}$ given by $\gamma_1(t)=3-e^{\pi it}$:
$\hspace{5cm}$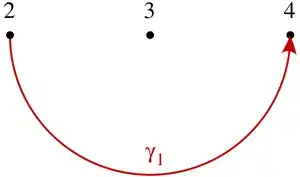
If we integrate along $\gamma_1$, we get
$$
\begin{align}
\int_{\gamma_1}\frac{\mathrm{d}y}{y-3}
&=\int_0^1\frac{-\pi i\,e^{\pi it}\,\mathrm{d}t}{-e^{\pi it}}\\
&=\pi i\tag{6}
\end{align}
$$
By Cauchy's Integral Theorem, any path from $2$ to $4$ that does not pass over $3$ will give the value $\pi i$.
However, we also have the path $\gamma_2:[0,1]\to\mathbb{C}$ given by $\gamma_2(t)=3-e^{-\pi it}$:
$\hspace{5cm}$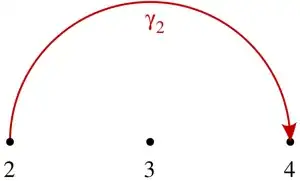
If we integrate along $\gamma_2$, we get
$$
\begin{align}
\int_{\gamma_2}\frac{\mathrm{d}y}{y-3}
&=\int_0^1\frac{\pi i\,e^{-\pi it}\,\mathrm{d}t}{-e^{-\pi it}}\\
&=-\pi i\tag{7}
\end{align}
$$
By Cauchy's Integral Theorem, any path from $2$ to $4$ that does not pass under $3$ gives the value $-\pi i$.
In fact, the integral of $\frac1{y-3}$ along any path between two points, $a$ and $b$, will differ by an integer multiple of $2\pi i$ from the integral along any other path between $a$ and $b$. This is because of the residue of $\frac1{y-3}$ at $y=3$. To have a well-defined anti-derivative of $\frac1{y-3}$, we need to make a branch cut that prevents a path from circling $3$.
For example, if we make the branch cut along $3+i[0,\infty)$, we allow $\gamma_1$. In this case, for $y\in\mathbb{R}$,
$$
\log(3-y)-\log(y-3)=\left\{\begin{array}{}
-\pi i&\text{if }y\gt3\\
+\pi i&\text{if }y\lt3
\end{array}\right.\tag{8}
$$
and the two anti-derivatives differ by a constant (which can be incorporated into the constant of integration).
However, if we make the branch cut along $3-i[0,\infty)$, we allow $\gamma_2$. In this case, for $y\in\mathbb{R}$,
$$
\log(3-y)-\log(y-3)=\left\{\begin{array}{}
+\pi i&\text{if }y\gt3\\
-\pi i&\text{if }y\lt3
\end{array}\right.\tag{9}
$$
and the two anti-derivatives differ by a constant (which can be incorporated into the constant of integration).
With such a branch cut, Cauchy's integral theorem guarantees $\int\frac{\mathrm{d}y}{y-3}$ can be well-defined on the rest of $\mathbb{C}$.

