Troubles figuring out how to calculate the centroid for a defuzzification process

Question

I am trying to implement a fuzzy logic system, but am having serious issues finding the centroid for the defuzzification process.

This is what my output sets look like:

My reference source gives this to me as an example:

This is going to sound silly, but unfortunately I cannot understand why he uses certain values for the calculation, I mean, how does he chose which values from the x axis to multiply with the ones from the y axis. For example, he has at some point (0.75*5), now how come he can't have (0.75*4)? There is no rule telling me I have to calculate every x axis member that is a multiplication of 5, but yet all the examples show me to do this, without really explaining.

A second example I found, tells me to do this:

This is, a much simpler calculation without the values in between. Unfortunately whenever I try to recreate the examples using both these methods, my results aren't matching what they are supposed to.

So to sum it all up, can someone please explain me exactly how you calculate the centroid for a deffuzification process?

Thank you very much for your time.

Answer 1

The first answer is that using ultra-precision on fuzzy calculations is a waste of time. Approximate answers are good enough for fuzzy sets.

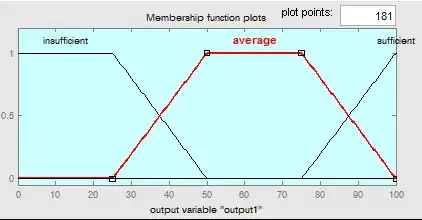
In your first example, the author has taken a set of evenly spaced samples and approximated the centroid of the full region with the centroid of the samples (as if the region were not distributed, but were just masses sitting at 0, 5, 10, 15, ...).

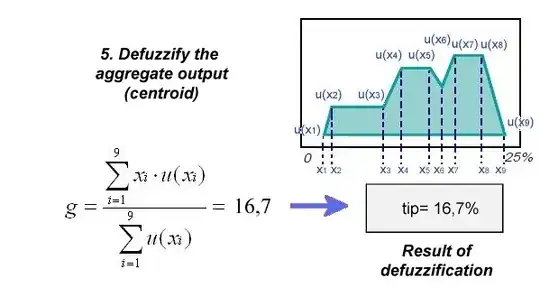
In your second example, the author has again approximated. This approximation is not very good. Note that the second example's estimate of the centroid of just the region over $[x_1,x_2]$ is as if all the mass were concentrated at $x_2$.

It is worth pointing out that both of these are approximations, both have drawbacks, and both are generally fine for getting useful results in practical systems. This does not mean that they are the best possible results.

The summation in your second example hints to the correct method. The centroid of the region bounded by $I=[x_1,x_2]$, the function $y(x)$ taking points of $I$ to real numbers, and the $x$-axis is $$\frac{\int_{x_1}^{x_2} x f(x) \mathrm{d}x}{\int_{x_1}^{x_2} f(x) \mathrm{d}x}$$. This is overkill, especially if your functions are piecewise linear (which your output and examples are). For your output set and both examples, it would be better to follow this recipe:

• For each rectangle, replace it with a mass at its (horizontal) midpoint equal to its width times its height. (At $\frac{1}{2}x_2 + \frac{1}{2}x_3$ we have mass $(x_3-x_2)u(x_2)$. We could use $u(x_3)$ as well since they're equal.)
• For each triangle, replace it with a mass two-thirds of the way from the tip to the spine. In the second example, this would be at $\frac{2}{3}x_2 + \frac{1}{3}x_1$. The mass is one half the width ("the base") times the height.
• Decompose each trapezoid (see $[x_3,x_4]$ in the second example) into the rectangle sitting on the $x$-axis and the triangle sitting above the rectangle. Replace the pair with the mass for the triangle and the mass for the rectangle. (I.e., we get two contributions -- one for the rectangle at the midpoint and one for the triangle $2/3$ of the way along.)

Use these locations as the $x_i$ and weights as the $u(x_i)$ in either of your formulae.

This overprecise method computes the exact centroids of piece-wise linear regions.