Is there a geometric interpretation of the line integrals :
$\int_{\gamma} f(x,y)\, dx$
$\int_{\gamma} f(x,y)\, dy$
(which should not be confused with $\int_{\gamma} f(x,y)\, ds$)
where the function $f(x,y)$ to be integrated is evaluated along a curve $\gamma$ ?
I'm not familiar with such line integrals, but I would think that one could interpret
$$\int_{\gamma} f(x,y)\, dx$$
as the area of the projection on the x-axis of the sheet defined by $f(x,y)$ evaluated along $\gamma$. Similarly, I would interpret
$$\int_{\gamma} f(x,y)\, dy$$
as the area of the projection on the y-axis of the sheet defined by $f(x,y)$ evaluated along $\gamma$.
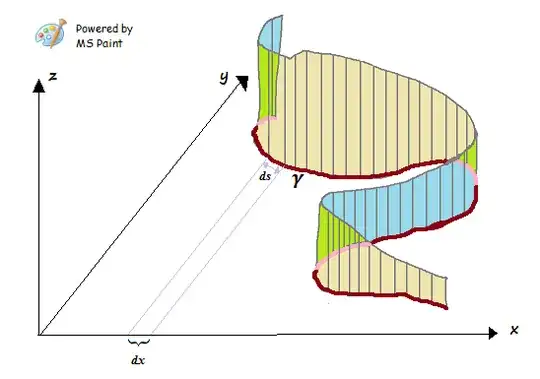
Assuming that we follow $\gamma$ from the lower right (see diagram), integrating with respect to $dx$ (along $\gamma$) will yield negative areas if the yellow side is exposed (to the $x$-axis), and positive areas if the blue side is exposed. Of course portions of $\gamma$ that run parallel to the $y$-axis wouldn't contribute anything to $$\int_{\gamma} f(x,y)\, dx$$
A line integral of the form $\int_\gamma f(x,y)\,dx$ is simply the line integral of the vector field $\vec F(x,y) = f(x,y)\vec i$ over $\gamma$, so if you understand the geometric interpretation of line integrals of vector fields you have your answer. Similarly for a line integral with respect to $dy$.
