4

Could someone kindly point me to references on constructing magic squares of even order? Does a compact formula/algorithm exist?

J. M. ain't a mathematician
  • 76,540
Computist
  • 525
  • I remember, I have seen only of odd order...even ordered exists..? – Tapu Oct 27 '11 at 18:37
  • 1
    @Swapan: Yes: there exist magic squares of any order except $2\times 2$. There are many direct algorithms for odd order magic squares, and if you can do a $k\times k$ and an $m\times m$, then you can do the $km\times km$ by dividing it into an $m\times m$ array of $k\times k$ squares (or a $k\times k$ array of $m\times m$ squares), and solving each of them as the $k\times k$, in the order given by the $m\times m$. This deals recursively with any $n$ not congruent to $2$ modulo $4$. – Arturo Magidin Oct 27 '11 at 19:53
  • @Arturo, thanks! I read (when I wrote this comment) about the existence from Wikipedia. – Tapu Oct 27 '11 at 21:43
  • @Swapan: I also missed that you need to deal with the $4\times 4$ and the $8\times 8$ directly. – Arturo Magidin Oct 28 '11 at 04:56
  • 1
    An algorithm for generating even-order magic squares due to Collison is presented here; if you have MATLAB, you can try to find the file magic.m to see the algorithms internally used (discussed briefly here). – J. M. ain't a mathematician Oct 28 '11 at 09:36

2 Answers2

4

A very elegant method for constructing magic squares of singly even order $n=4m+2$ with $m\geq1$ is due to J. H. Conway, who calls it the "LUX" method.

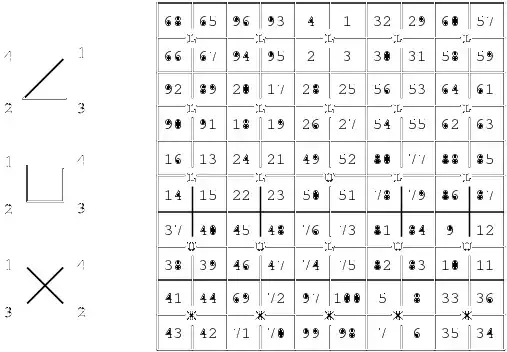
Create an array consisting of $m+1$ rows of Ls, $1$ row of Us, and $m-1$ rows of Xs, all of length $n/2=2m+1$. Interchange the middle U with the L above it. Now generate the magic square of order $2m+1$ using the Siamese method centered on the array of letters (starting in the center square of the top row), but fill each set of four squares surrounding a letter sequentially, according to the order prescribed by the letter. That order is illustrated on the left side of the figure below, and the completed square is illustrated to the right. The "shapes" of the letters L, U, and X naturally suggest the filling order, hence the name of the algorithm.

This example should illustrate the "LUX" method:

LUX demo

EDIT:

An method for constructing magic squares of doubly even order $n=4m$ is to draw Xs through each $4×4$ subsquare and fill all squares in sequence. Then replace each entry $a_{(ij)}$ on a crossed-off diagonal by $(n^2+1)-a_{(ij)}$ or, equivalently, reverse the order of the crossed-out entries. Thus in the below example for $n=8$, the crossed-out numbers are originally $1, 4, ..., 61, 64,$ so entry $1$ is replaced with $64$, $4$ with $61$, etc.

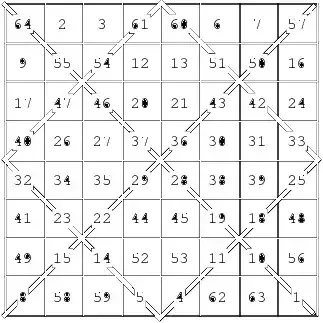
doubly even example

Dave Everitt
  • 103
Pedja
  • 13,292
3

This is 2 years old but here are some new results.

A new/revised class of algorithms for single-even/double-even magic squares can be found on arXiv:

http://arxiv.org/ftp/arxiv/papers/1202/1202.0948.pdf

Nikos M.
  • 31