3

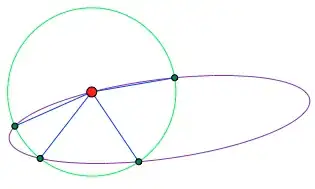
Similar to Point on circumference a given distance from another point, but for an ellipse. Unfortunately, the difference is non-trivial.

I have an ellipse and a point (C) that is somewhere on the ellipse. I would like to determine the location of some other point on the ellipse away from that point, in one direction (A) or the other (B) by a given straight-line distance (r). This is apparently equivalent to finding the intersections between the ellipse and a circle C with radius r.

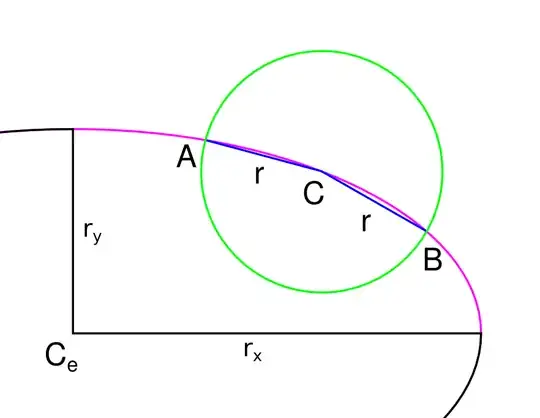
Illustration of intersecting ellipse and circle

In the following, please consider a "point" to mean "the Cartesian coordinates of a point".

Known:

  • An ellipse defined in terms of center point Ce and radius lengths rx, ry
  • A point C on the ellipse (or, equivalently, the angle of the ray from Ce through C)
  • A distance r (r > 0)
  • The direction of rotation, either clockwise or counterclockwise

Unknown:

  • A point on the ellipse in the given direction from C that is also a distance of r from C along a straight line (or, equivalently, the angle of the ray from Ce to said point); specifically,
    • A, if the direction of rotation is counterclockwise.
      • Update: If there are multiple candidates for A, the candidate whose segment aligns most closely with the ellipse is selected. (If I'm not mistaken, an A candidate can be said to align more closely with the ellipse if the area between the segment and the counterclockwise arc it crosses, starting at C, is smaller than that of another candidate. There are probably other measures for this determination.)
    • B, if the direction of rotation is clockwise
      • Update: If there are multiple candidates for B, the candidate whose segment aligns most closely with the ellipse is selected. (If I'm not mistaken, a B candidate can be said to align more closely with the ellipse if the area between the segment and the clockwise arc it crosses, starting at C, is smaller than that of another candidate. There are probably other measures for this determination.)

Intuitively, there is some rmax for each set of other inputs such that, for r = rmax, the result is the same in either direction (because the circle intersects with the ellipse in one point rather than two), and that for r > rmax, there is no solution (because there is no intersection at all).

I have failed to locate the formulae that implement this, but it's likely that I just didn't know what terminology to look for. Thoughts?

Update: As MvG points out below, I missed the cases where up to four intersections are possible. (I'd considered them, actually, but given only a shallow examination thought that this didn't apply if the center of the circle was on the ellipse. Oops.) Therefore, the direction may not uniquely identify a segment. Additional requirements are given above.

Community
  • 1
psmay
  • 133
  • 2
    It is a quartic polynomial that locates these intersections. Are you okay with type of answer, assuming an explicit polynomial from the problem data is provided? – hardmath Apr 07 '14 at 21:25
  • The algorithm may be more useful than the equation (read: it's for software), but I'll take what I can get. So…yes. – psmay Apr 08 '14 at 00:05

1 Answers1

3

You should consider the possibility that circle and conic intersect in four points:

Four points of intersection

So even if you know the direction, this might not be enough to uniquely define the solution you want. In any case, a circle is a special case of conic section, so a generalization of your problem is the task of intersecting two conic sections. This usually involves at least the task of finding roots of cubic polynomials. I can't see any approach where one conic being a circle would make things substantially easier, so I'd implement that generic approach and use it here.

Community
  • 1
MvG
  • 44,006
  • Duly noted. For the purposes of this process, only the two segments that align most closely with the ellipse would be correct (the leftmost and rightmost points in your image, but not the two between). Is there any accounting for that? – psmay Apr 08 '14 at 18:41
  • Updated the question to mention the additional requirement. Thanks. – psmay Apr 08 '14 at 19:00
  • @psmay: Computing only two of these points is not fundamentally easier than computing all four. You still have to solve a cubic equation. Once you have all four points, you can use e.g. distance from a tangent line to identify the relevant ones. – MvG Apr 08 '14 at 19:34
  • Why cubic? As you note there are four roots, potentially all real. Are you thinking of the auxiliary cubic to solve a quartic? – hardmath Apr 09 '14 at 11:51
  • @hardmath: I'm thinking of the cubic used in step 2 of this approach. If that's the “auxiliary cubic” you refer to, then yes, but I'm not sure what exactly you mean there. – MvG Apr 09 '14 at 12:00