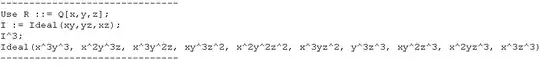5

I am trying to determine the set that generates a monomial ideal. Namely, the ideal $(xy,yz,xz)^3$.

I know it will have terms $x^3y^3$, $z^3y^3$, $x^3z^3$. For the other terms that generate, I do not know how to determine them (it should be some sort of combination of two of the terms, such that their powers sum to 6, correct?)

Also, is mathematica able to compute this?

user26857
  • 53,190
user138864
  • 233

1 Answers1

1

$I = (xy,yz,xz)$ is generated by the monomials $u_1,u_2,u_3$. so $I^3$ is generated by all the products of $3$ (not necessarily distinct) monomials from the set $\{u_1,u_2,u_3\}$. so $I^3$ has the generators
$$\{(x^ay^bz^c); a+b+c=6; \ 0 \le a,b,c \le3 \}$$

I dont know about mathematica, but CoCoA has:
enter image description here

user 1
  • 7,652