On the "solvability" of jigsaw Sudoku puzzles

Question

I am making a computer program that is going to generate Sudoku puzzles of various types. One of these types is "jigsaw", in which the board is split into rows, columns and random 9-square contiguous regions. My regions are generated completely randomly and I have become concerned that maybe there are some arrangements of region for which no solution can exist. Can anybody give me an example of this or perhaps explain why no such arrangement exists. Thank you.

When you say 'no solution can exist', do you mean 'it can be shrunk down to a sudoku puzzle that can't be solved', or do you mean 'there is no Latin Square assignment that makes certain that each jigsaw region contains the numbers 1-9'? — Steven Stadnicki, Mar 22 '14 at 18:50
@maxG795 Are your contiguous regions completely disjoint, and not necessarily 3 x 3 boxes? And are there exactly 9 regions, so that the regions cover the entire board? — Caleb Stanford, May 20 '14 at 05:29
For a related question, please see: https://puzzling.stackexchange.com/questions/117050/tiling-a-5x5-square-with-five-pentominoes-and-a-latin-square — Will.Octagon.Gibson, Jan 03 '25 at 06:55

score 2 · Answer 1 · answered Jan 03 '25 at 06:49

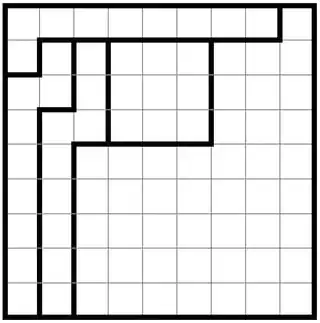
There are some choices for the nine random 9-square contiguous regions such that no valid Jigsaw Sudoku is possible.

For example, consider the following partially subdivided $9 \times 9$ grid.
No matter how the rest of the grid is subdivided, we won’t get a valid Jigsaw Sudoku.

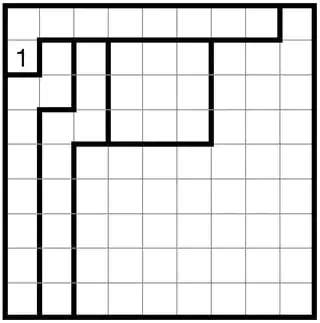
Let’s fill in the number that is at the start of row 2.

Without loss of generality, we can assume this number is a 1:

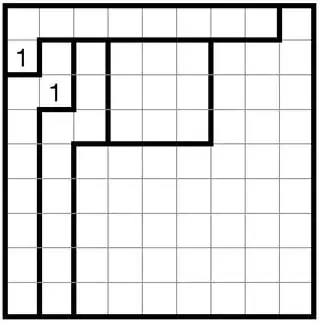
For the region that occupies columns 1 and 2, there is only one possible square that can contain a 1:

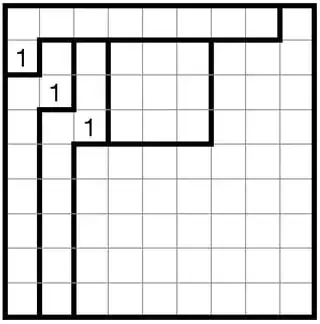
Similarly, for the region that occupies columns 2 and 3, there is only one possible square that can contain a 1:

And now we have a problem; for the square $3 \times 3$ region there is no square that can contain a 1.

On the "solvability" of jigsaw Sudoku puzzles

1 Answers1