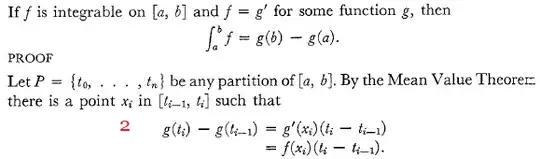1

1. How can we presage to use Mean Value Theorem to start the proof?

2. Mean Value Theorem engenders a point in an open interval. Shouldn't this be $x_i \in (t_{i - 1}, t_i) $?

After reading LittleO's post I discovered intuition at artofproblemsolving.com.

enter image description here

Community
  • 1

2 Answers2

2

The intuition for the (second) fundamental theorem of calculus is that \begin{equation} \text{"the total change is the sum of all the little changes".} \end{equation}

The total change is $g(b) - g(a)$. The little changes are \begin{equation*} g(t_i) - g(t_{i-1}) \approx g'(\xi_i)(t_i - t_{i-1}) \end{equation*} (where $\xi_i$ is any point in $[t_{i-1},t_i]$.)

By adding up all the little changes, you get the total change. \begin{align*} g(b) - g(a) &= \sum g(t_i) - g(t_{i-1}) \\ &\approx \sum g'(\xi_i)(t_i - t_{i-1}). \end{align*} Notice that this last expression is a Riemann sum for the integral $\int_a^b g'(t) \, dt$.

It's wonderful that the mean value theorem allows us to replace the approximate equalities with exact equalities, which helps us turn this intuitive argument into a rigorous proof.

littleO
  • 54,048
  • thanks. +upvote. i linked to http://www.artofproblemsolving.com/Wiki/index.php/Fundamental_Theorem_of_Calculus. do you understand my questions 1 and 2? please apprise me? –  Mar 13 '14 at 14:03
  • For question 1, we first come up with the intuitive argument, and then we recognize that the mean value theorem allows us to write $g(t_i) - g(t_{i-1}) = g'(\xi_i)(t_i - t_{i-1})$, with equality rather than approximate equality. This is clearly a helpful step towards a rigorous proof. For question 2, yes the mean value theorem gives you a point in $(t_{i-1},t_i)$. – littleO Mar 13 '14 at 22:23
0
  1. You have a function $g$ and you know nothing about it except that it is differentiable on an interval, and you want to show something about its behaviour in that interval. The mean value theorem is a good bet.
  2. If $x_i \in (t_{i-i},t_i)$ then $x_i \in [t_{i-i},t_i]$ so the statement is not wrong.
  3. If you start driving your car at time $a$ and stop at time $b$, and your speedometer is printing out a graph of your speed over time given by $f(t)$, and your odometer is printing out a graph of the distance that you've travelled given by $g(t)$, then the total distance that you travel $g(b)-g(a)$ is equal to the area under the graph of $f$ from $a$ to $b$.
crf
  • 5,679
  • thanks. +upvote. please expatiate on 1? i don't understand why mvt is "a good bet." 3. this example requires $f(t)$ continuous? but this theorem posits only integrable? –  Mar 13 '14 at 14:00
  • @TuckerRapu $f$ can be discontinuous. MVT is a very powerful theorem that you can use to prove all kinds of things about the behaviour of a differentiable function on an interval. As littleO explains, we can get to $g(b)-g(a)\approx \sum g'(x_i)(t_i - t_{i-1})$ for some $x_i$ in the interval without appealing the the mean value theorem. Now we want to tighten that $\approx$ to an $=$, that is, we want to write $g(b)-g(a) = \sum g'(x_i)(t_i - t_{i-1})$... – crf Mar 13 '14 at 17:47
  • But this clearly does not necessarily hold for all $x\in (t_i - t_{i-1})$'s, so we need to show that there is an $x_i$ in each interval such that it holds. But that is exactly what the mean value theorem promises. – crf Mar 13 '14 at 17:48