3

How do I prove that the derivative of $\sin$ is $\cos$ without resorting to L'Hôpital's rule (circular logic)?

This part is easy:

$$ \begin{align*} \sin'(x) &= \lim_{\Delta x \to 0} \frac{\sin(x + \Delta x) - \sin(x)}{\Delta x} \\ \sin'(x) &= \lim_{\Delta x \to 0} \frac{\cos(x)\sin(\Delta x) + \sin(x) \cos(\Delta x) - \sin(x)}{\Delta x} \\ \sin'(x) &= \lim_{\Delta x \to 0} \left(\cos(x)\frac{\sin(\Delta x)}{\Delta x} + \sin(x)\frac{\cos(\Delta x) - 1}{\Delta x}\right) \\ \end{align*} $$

but where do I go from here?

user541686
  • 14,298
  • I'm tempted to suggest Taylor series... but there should be some way without using it... – 2012ssohn Mar 11 '14 at 01:20
  • @2012ssohn: How do you obtain the Taylor series? – user541686 Mar 11 '14 at 01:21
  • @2012ssohn Yeah... –  Mar 11 '14 at 01:21
  • @Mehrdad The Taylor series is obtained by taking the derivative, when one is first introduced to them - you do, for $f(x)$ about $a$, $f(x)\approx\sum^{\infty}_{i=0}\dfrac{f^{(i)}(a)}{i!}(x-a)^i$. –  Mar 11 '14 at 01:22
  • @SanathDevalapurkar: Sure, but how do you obtain the derivative then? – user541686 Mar 11 '14 at 01:22
  • @Mehrdad From the limit, so in a way, this, too is circular. –  Mar 11 '14 at 01:22
  • @SanathDevalapurkar: Yeah, that's my point. Taylor series would be completely circular logic. – user541686 Mar 11 '14 at 01:23
  • 1
    @Mehrdad - here you go. – 2012ssohn Mar 11 '14 at 01:23
  • @2012ssohn: Ooh thanks, that's really clever! You should post it as an answer! – user541686 Mar 11 '14 at 01:25
  • You could write sin in terms of complex exponentials and work with that. – Lost Mar 11 '14 at 01:25
  • 1
    Depends of your definition of sine. You can define the sine function as the function $\sin: \mathbb{R}\to \mathbb{R}$ by the formula $\sin(x):=\sum_{n=0}^\infty (-1)^n x^{2n+1}/(2n+1)!$. This is not circular. But depends of how do you define sine – Jose Antonio Mar 11 '14 at 01:26
  • @Lost: Great point, that works for me personally but I was more curious about how to do it when you don't already know more advanced math. Thanks though, I didn't think of that. – user541686 Mar 11 '14 at 01:28
  • @JoseAntonio: I'm using the geometric definition (ratio of a triangle's opposite side length to hypotenuse)... extended beyond 180 degrees I guess. I'm not looking for something that's more advanced than the problem statement. – user541686 Mar 11 '14 at 01:29
  • First try to show $\lim_{x\to 0: x\not= 0} \sin x/x=1$ – Jose Antonio Mar 11 '14 at 01:32

3 Answers3

5

Starting off where you finished and credits to this pdf:

$$\sin'(x) = \lim_{\Delta x \to 0} \left(\cos x \frac{\sin \Delta x}{\Delta x} + \sin x \frac{\cos \Delta x - 1}{\Delta x} \right)$$ $$= \cos x \lim_{\Delta x \to 0} \frac{\sin \Delta x}{\Delta x} - \sin x \lim_{\Delta x \to 0} \frac{1 - \cos \Delta x}{\Delta x}$$

Part I: prove that $\displaystyle \lim_{\Delta x \to 0} \frac{\sin \Delta x}{\Delta x} = 1$.

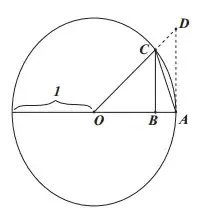
Assuming that $OA = 1$ (i.e. it's a unit circle), we have $\sin \theta = BC$. We then note that

[Area of triangle $AOD$] > [Area of sector $AOC$] > [Area of triangle $AOC$]

which means

$$\frac{1}{2} \frac{\sin \theta}{\cos \theta} > \frac{1}{2} \theta > \frac{1}{2} \sin \theta$$

From this we get $$\cos \theta < \frac{\sin \theta}{\theta} < 1$$

and since $\displaystyle \lim_{\theta \to 0} \cos \theta = 1$, we have that $\displaystyle \lim_{\theta \to 0} = 1$.

Part II: prove that $\displaystyle \lim_{\Delta x \to 0} \frac{1 - \cos \Delta x}{\Delta x} = 0$.

$$\lim_{\Delta x \to 0} \frac{1 - \cos \Delta x}{\Delta x} = \lim_{\Delta x \to 0} \frac{(1 - \cos \Delta x) (1 + \cos \Delta x)}{(1 + \cos \Delta x)\Delta x} = \lim_{\Delta x \to 0} \frac{1 - \cos^2 \Delta x}{(1 + \cos \Delta x)\Delta x}$$

$$ = \lim_{\Delta x \to 0} \frac{\sin^2 \Delta x}{(1 + \cos \Delta x)\Delta x} = \lim_{\Delta x \to 0} \frac{\sin \Delta x}{\Delta x} \frac{\sin \Delta x}{1 + \cos \Delta x}$$

We have proven in part I that $\displaystyle \lim_{\Delta x \to 0} \frac{\sin \Delta x}{\Delta x} = 1$, and we note that $\displaystyle \frac{\sin \Delta x}{1 + \cos \Delta x} = \frac{0}{1+1} = 0$.

We finally put all this together to get that $$\boxed{\displaystyle \sin'(x) = \cos x \lim_{\Delta x \to 0} \frac{\sin \Delta x}{\Delta x} - \sin x \lim_{\Delta x \to 0} \frac{1 - \cos \Delta x}{\Delta x} = \cos x \cdot 1 - \sin x \cdot 0 = \cos x}$$

ShreevatsaR
  • 42,279
2012ssohn
  • 3,865
1

Read this post, as it is very helpful: http://www.wyzant.com/resources/lessons/math/calculus/derivative_proofs/sinx

Since you are unsatisfied and do not understand the proof, I will further explain. As we learned in precalc, $\lim_{x\rightarrow 0} \frac{\sin x}{x} = 1$ and $\lim_{x\rightarrow 0} \frac{1- \cos x}{x} = 0 $. Please search a proof of these identities in another question if still confused, as that is a much simpler problem that can be solved using the squeeze theorum. Make these substitutions and you will have your answer.

louie mcconnell
  • 2,144
  • -1 for not understanding the question. – user541686 Mar 11 '14 at 01:27
  • Is this not what 2012ssohn posted? Exact same thinking. – louie mcconnell Mar 11 '14 at 01:39
  • "Exact same thinking"? Where in the site you linked to does it mention the squeeze theorem that 2012ssohn posted? – user541686 Mar 11 '14 at 01:46
  • I apologize for failing to mention the squeeze theorum; I made the incorrect assumption that you had already learned about the squeeze theorum and limits of the two functions mentioned above. By the time I was taking derivatives (calc), I had already learned those two identities in trig/precalc. My fault for not recognizing that you may have learned the information in a different order, or your school may have taught it in a different way. – louie mcconnell Mar 11 '14 at 01:52
0

In my introduction to limits, we used a lemma

\begin{equation} \lim_{x\rightarrow 0} \frac{\sin x}{x} = 1. \end{equation}

This was proved by drawing a picture and using the definition of the sine function and the definition of radians, along with the geometric "axiom" "the shortest distance between two points is a straight line segment".

That lemma can then be used to calculate $\lim_{x\rightarrow 0} \frac{1-\cos x}{x}$ and $\sin'(x)$.

aschepler
  • 11,035