1

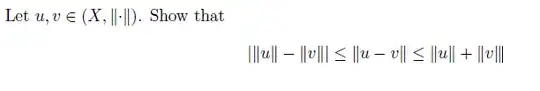
How to Prove this

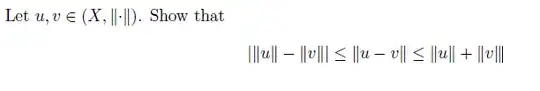
I tried proving this with triangular inequality but i was not right can any one help me with this

Yiorgos S. Smyrlis
  • 86,581
Nithish
  • 113
  • 12
  • 2
    Suggest improving the title to give a little more flavour to the question. "How to prove this" could be anything... – Assad Ebrahim Feb 17 '14 at 22:24
  • Also, why not present your work so far? It could be that your attempt goes wrong at a particular point, and it will be much more useful to you if people could point our where your error is. – Assad Ebrahim Feb 17 '14 at 22:26
  • Why the downvotes? – Asinomás Feb 17 '14 at 22:28
  • @user4140 Exactly,why the down votes ? – Nithish Feb 17 '14 at 22:32
  • yes, that's what I just asked. – Asinomás Feb 17 '14 at 22:33
  • This is a relatively simple problem. The fact that this had no title and no work (i.e. shows no real effort) goes against "Include details about what you have tried and exactly what you are trying to do." There are always plenty of people who are happy to just dash off a solution, but IMO it would be good to see a bit more effort from the poster -- and willingness to put up partial work. – Assad Ebrahim Feb 17 '14 at 22:34
  • @AssadEbrahim The reason why i posted here is i got struck at one point.I was not sure if i was correct. – Nithish Feb 17 '14 at 22:35
  • But he does kind of explain he tried using triangle inequality. And, he's a new user,perhaps he wasn't aware that title is very weak. – Asinomás Feb 17 '14 at 22:36
  • He's got his answers and I've expressed my opinion. The community is more than welcome to express theirs -- in upvotes -- if they wish. – Assad Ebrahim Feb 17 '14 at 22:38

3 Answers3

6

The first

$$||u-v||=||u+(-v)||\le ||u||+||-v||=||u||+||v||$$ and the second

$$||u||=||u-v+v||\le ||u-v||+||v||\Rightarrow ||u||-||v||\le ||u-v||$$ and by symmetry we have the other inequality so we conclude.

2

We simply use the triangular inequality repeatedly: $$ \|u\|=\|(u-v)+v\|\le \|u-v\|+\|v\|, $$ and thus $$ \|u\|-\|v\|\le \|u-v\|\le \|u\|+\|-v\|=\|u\|+\|v\|. \tag{1} $$ Similarly $$ \|v\|=\|(v-u)+u\|\le \|v-u\|+\|u\|, $$ and thus $$ \|v\|-\|u\|\le \|u-v\|. \tag{2} $$ Now $(1)$ and $(2)$ imply that $$ \big|\|u\|-\|v\|\big|\le \|u-v\|\le \|u\|+\|v\|. $$

Yiorgos S. Smyrlis
  • 86,581
1

Hint:

  1. $\left\|u\right\| = \left\|(u-v)+v\right\|$
  2. $\left\|v\right\| = \left\|(u-v)+u\right\|$
  3. $\left\|u-v\right\| = \left\|u+(-v)\right\|$
user127.0.0.1
  • 7,435