7

This question is to help me find peace.

First, the question of the Snowflake's compactness has been tackled here on this site:

But I'm inclined to believe it is not. The only reason Henning Makholm's argument does not fully convince me is because I believe I can come up with an open cover without finite subcover. What you do is surround each triangle with an open triangle small enough so that it doesn't intersect the 'sprouts' two levels down which sprouted out of the first iteration, and then repeat that ad infinitum. I hope this picture helps (the grey lines represents the open sets):

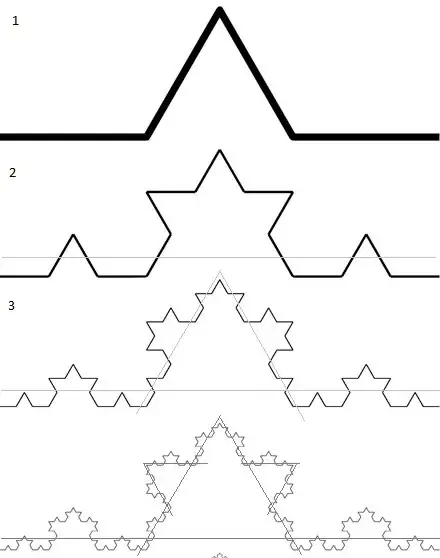
enter image description here

So, my question is why does this open cover have a finite subcover?

Community
  • 1
  • What exactly is your cover? Are you sure that you've covered the point $(1/3,0)$? – Mark McClure Feb 13 '14 at 02:44
  • I've only posted one side of the original triangle. The grey lines implicitly connect by a straight line on the 'inside.' And I implicitly did this pattern to each triangle. –  Feb 13 '14 at 02:48

2 Answers2

10

It's not an open cover. Take a point of a "sprout" that is not in open set number $n$. These can be chosen to converge (and in any case some subsequence must converge). The limit is in the snowflake but not in any of your open sets.

Robert Israel
  • 470,583
  • I can see how you can do that, but instead of making me think that I don't have an open cover, it makes me believe the Snowflake does not have some of its limit points. Every point of the Snowflake belongs to some iteration, right? –  Feb 13 '14 at 02:53
  • 6
    Well, that's your mistake right there. No, the Snowflake is the set of limit points of the iterations. – Robert Israel Feb 13 '14 at 03:07
  • 1
    @Bryan In fact the only points of the iterations that are also part of the Snowflake are those points that are a corner at some iteration (and then of course also at all following iterations). These form only a countable set of points of the curve, but because the are the image of a dense subset of the parameters, they do determine the whole Snowflake by continuous interpolation. – Marc van Leeuwen Feb 13 '14 at 12:25
4

The curve is the image of a continuous function over the set $[0,1]$ as you can see in the answer that you post. Therefore, as compactness is preserved under continuous functions, the Koch curve is compact.

Community
  • 1
amaurs
  • 258
  • I knew that the space was compact and why it was. My question was about the 'cover.' I've edited the title to make it more clear. –  Feb 13 '14 at 05:32