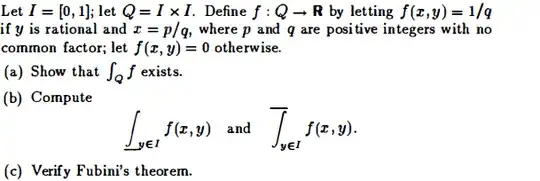0

Question

This is from Munkres Analysis on Manifolds book (have only done Reimann Integral and definition of Measure 0).

I am stuck on part a). I was thinking that possibly we have to show that the set of discontinuities have measure 0. Following from Thomae's Function, it seems that the function should not be continuous at tuples (rational,rational). From here on, however, I have no idea on how to proceed with the problem. Any help or hints are appreciated.

user52932
  • 403
  • 1
    The points of the form $(p/q,\text{irrational})$ have points of the form $(p/q,\text{irrational})$ and $(p/q,\text{rational})$ arbitrarily near, so $f$ can't be continuous on those either. If the first coordinate is irrational, though, the value of the function will be forced to approach $0$ as the $x$ coordinate approaches the irrational number, so those are points of continuity. – dafinguzman Feb 09 '14 at 12:04
  • So how would I go about showing that the set of points of discontinuity have measure 0? I would have to show that for any epsilon there exist a sets (countably many) whose total volume is less than epsilon and they cover the set of discontinuity. – user52932 Feb 09 '14 at 18:33
  • 1
    The set of tuples the form $($rational, rational$)$ is countable, so its Lebesgue measure is $0$. For each rational $r$, the set $S_r={(r,y): y \text{ irrational}}$ has product measure $0$, because it is the cartesian product of a set of measure $0$ (the singleton $r$) with a set of finite measure $\mu$. To conclude, notice that $\cup _r S_r$ is a countable union of sets of measure $0$. – dafinguzman Feb 09 '14 at 23:14
  • Okay. One question though: it is true that points of form (p/q,irrational) have points of form (p/q, rational), (irrational , irrational) and (p/q, irrational) around it. Now (p/q,irrational) gets mapped to 0. This is also true for nearby points of form (p/q, irrational) and (irrational , irrational). So the only potential problem are the points of the form (p/q, rational). These points get mapped to 1/q. But there are only finitely many points of form p/q with denominator as big as q in any interval. So select a $\delta$ such that these points lie outside the $\delta$-ball. – user52932 Feb 11 '14 at 19:50
  • Then, we can decrease $\delta$ so that 1/q approaches 0. So the function remains continuous at these points. (This is how we show that Thomae's Function is continuous at irrationals). It seems to me that the discontinuity would only be at pints of form (p/q, rational) and these have measure 0. – user52932 Feb 11 '14 at 19:51
  • The $\delta$-ball would now contain points of form (p/q,irrational) where for every p/q, $q>q_0$. – user52932 Feb 11 '14 at 19:58
  • You are analyzing continuity at a point, say $(p/q,y)$, with $y$ irrational. If you fix $p/q$ and make the second variable $z$ approach $y$, $z$ will be rational and irrational arbitrarily close to $y$, making the function oscillate between the values $1/p$ and $0$ near $(1/p,y)$. – dafinguzman Feb 11 '14 at 19:58
  • okay. I see. Do you know that how would I establish continuity at points of form (irrational, irrational) and (irrational, rational). Because I would have to show that these two sets of (rational, rational) and (rational, irrational) compose the set of discontinuity. – user52932 Feb 11 '14 at 20:02
  • Continuity in the case that the first variable is irrational is easy, it's just like in Thomae's function: the only cases that you worry about are those where the function is equal to $1/q$ near the point, and $q$ (which only depends on the first coordinate) is going to become infinite as the first coordinate approaches the irrational point. – dafinguzman Feb 11 '14 at 20:21
  • So the only points I need to worry about are (irrational, irrational) and (irrational, rational) and both should have a proof similar to Thomae's function. I didn't understand the part that you said I need to worry about. – user52932 Feb 11 '14 at 21:47

1 Answers1

1

In what follows, $p$ and $q$ will denote positive integers with no common factor, $r,s$ will be rational numbers, $i$ will be an irrational number, and $x,y,z$ will be arbitrary real numbers.

The function is defined by $f(\frac pq,r)=\frac 1q$, $f=0$ otherwise. I claim that $f$ is discontinuous on the points $a$ which have a rational first coordinate and continuous on the points $b$ which have an irrational first coordinate.

Discontinuity. Fix $p$ and $q$ and suppose the point is of the form $a=(\frac pq,y),$ for some real $y$. In any neighborhood of $a$ there are points of the form $(\frac pq,r)$ and $(\frac pq,i)$. It follows that in any neighborhood of $a$ the function takes the values $f(\frac pq,r)=\frac 1q$ and $f(\frac pq,i)=0$, so $\lim_{(x,y)\to a} f(x,y)$ doesn't exist.

Continuity. Now suppose $b=(i,y)$ for some real $y$, so that $f(b)=0$, and let $g(u)$ be Thomae's function. $g(u)$ is continuous at the irrationals $i$, so we know that given a positive $\epsilon$ there exists some positive $\delta$ such that, whenever $|i-u|<\delta$, $|g(u)|<\epsilon$.

Now, take that same $\delta$. If $|(i,y)-(u,v)|<\delta$, then in particular $|i-u|<\delta$. There are two possibilities: either $f(u,v)=0$ or $f(u,v)=g(u)$. In either case, following the property of $\delta$, $|f(u,v)|<\epsilon$, so that $f$ is continuous at these points.

What I tried to say in the comments, intuitively, is that in any neighborhood of $b$ you will find points which map to $0$ and points which map to $\frac 1q$ for some $q$, but as the first coordinate inevitably approaches an irrational number, those values of $q$ will be forced to approach infinity. I hope that the argument presented made this intuition clear.

Finally, the segments $S_r=\{(r,y): 0\leq y\leq 1\}=\{r\}\times [0,1]$ have product measure $0\cdot 1=0$, so that the set of points of discontinuity $\cup_{r\in \mathbb Q} S_r$ has measure $0$.

dafinguzman
  • 3,497
  • Thanks a lot. Is there a way to explicitly show that product measure is 0 just by using the definition of measure 0. The only definition that I am allowed to use is the definition of measure 0. The definition I have is that a set has measure 0 if for every $\epsilon$ you can cover it with countably many rectangles such that the total volume of rectangles is less than $\epsilon$. I am trying to think of how to cover $S_r$ with such rectangles but am not having any success. – user52932 Feb 12 '14 at 00:09
  • Maybe try the rectangles $[r-\epsilon/2,r+\epsilon/2]\times[0,1]$. If you want to cover them all in one go, enumerate the rationals ${r_k}$ and cover each segment $S_r$ by a rectangle of length $\epsilon/2^k$. – dafinguzman Feb 12 '14 at 03:19
  • I'm sorry, open rectangles. – dafinguzman Feb 12 '14 at 04:37
  • Ok thanks. Part c) is super easy. Part b) the lower integral is obvious and should equal 0. The upper integral defined as infimum(U(f,P)) over all partitions P, where U(f,P) is the upper reimman sum should equal 0. Do I have to use a similar argument of how as partition size decreases, the infimum of U(f,P) will equal 0 because 1/q will approach 0. – user52932 Feb 12 '14 at 04:43
  • Yes, that's it. For any $\epsilon$ you have to show that there is a partition $P$ such that $U(f,P)<\epsilon$. You can inspire yourself in the same argument for Thomae's function. – dafinguzman Feb 12 '14 at 05:19
  • Okay I seem to have an answer but I am slightly confused. Just to confirm, in our case, the $x$ is fixed because the integral is over $y$. So what we want is to consider the upper Riemann sum as $y$ varies - only in the case where $x$ is a fixed rational because otherwise the upper integral is trivially 0. This value fluctuates between 1/q (which is fixed) and 0 depending on y. So we want to construct a partition that in such a scenario, the upper reimann sum is less than epsilon. – user52932 Feb 12 '14 at 06:39
  • The Thomae's function argument works if we integrate over x – user52932 Feb 12 '14 at 06:42
  • I guess I am having difficulty because there are infinitely many rationals in the intervals of a partition and so the function seems to be taking the value 1/q (a fixed number) at infinitely many points. I don't see a way around this. – user52932 Feb 12 '14 at 06:51
  • You are integrating over $x$ and $y$. So you need to make partitions in both axes. I gave the link with the case of Thomae's function so that you can get the idea of how to partition the $x$ axis. The partition of the $y$ axis won't be a problem: actually you could make the trivial partition $(y_0=0, y_1=1)$ in the $y$ axis and things would work out well. Think about it: the Riemann sums that you have to form will be something like $\sum\sum f(x_i, y_j)\Delta x_i \Delta y_j$. The trivial partition in $y$ will trivialize the sum in $j$ and $\Delta y$ will just be $1$. – dafinguzman Feb 12 '14 at 07:05
  • Oh. But I thought that in part b) of the question, since the question asks us to compute $\displaystyle \int_{y\in I} f(x,y)$, i just want to fix $x$ and integrate over y. – user52932 Feb 12 '14 at 07:11
  • Oh, sorry for that! my mistake. – dafinguzman Feb 12 '14 at 07:12
  • But if I make the trivial partition, how would things work out. The width would be 1. so Reiman sum would equal 1/q (because there is only 1 Rectangle). I want it to equal 0 (i think 0 is the correct answer). – user52932 Feb 12 '14 at 07:13
  • Then if $x$ is irrational, you're done and the integral is $0$. If $x$ is $p/q$, then $f(y)=1/q$ for $y$ rational and $0$ for $y$ irrational. That would mean that the upper integral is just $1/q$ in this case, because you will find points which map to $1/q$ in any subinterval of any partition and the lengths of the subintervals sum to $1$. – dafinguzman Feb 12 '14 at 07:18
  • let us continue this discussion in chat – dafinguzman Feb 12 '14 at 07:18