3

Sangaku (算額) are Japanese geometric puzzles written on wooden tablets over 150 years ago. There have been several previous puzzles, but I didn't see this one.

Find the radii of the two inner circles in terms of $x$:

Sangaku Image

Jean-Claude Arbaut
  • 23,601
  • 7
  • 53
  • 88
jmac
  • 191

1 Answers1

4

Let the radius of the smaller circle be $r$, and the larger be $R$. It is immediately obvious that $r$ satisfies $$(x-r)^2 + (x/2)^2 = (r+x)^2,$$ and $R$ satisfies $$(x/2+R)^2 + (x/2)^2 = (x-R)^2.$$ The solutions of these are a straightforward algebraic exercise.

Slightly less trivial would be finding the radius of the circle inscribed in either of the two "ear-shaped" regions (inside the semicircle and one of the two quarter circles, but outside the other quarter circle). However, it too is amenable to the same solving technique.

Addendum. Since an image was requested, I have attached it below: 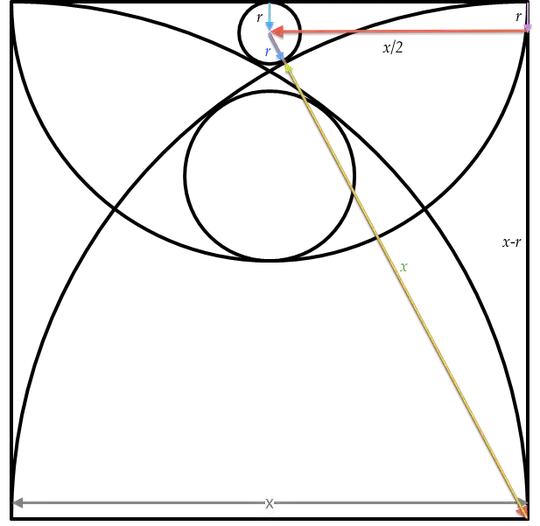enter image description here The horizontal red line has length $x/2$, and the diagonal line has length $r+x$, since it joins the centers of two tangent circles with radius $r$ (blue) and $x$ (green/yellow). The third side is simply $x - r$, because the red horizontal line is parallel to the top edge of the square.

An analogous procedure for the larger circle results in the second equation. It really does not get any easier than that.

heropup
  • 143,828
  • What is $x$ in your solution? – Nathaniel Bubis Jan 31 '14 at 07:00
  • As shown in the diagram, $x$ is the side length of the square. – heropup Jan 31 '14 at 07:00
  • Sorry, I think I'm a bit dim here and/or I need a bit more explanation (which you are of course not obligated to give). Where are you getting these formulas from? Any chance you could attach some words to the concept here, because I have absolutely no idea where these came from. – jmac Jan 31 '14 at 07:03
  • @jmac, elementary analytic geometry after choosing a system of coordinates. – Martín-Blas Pérez Pinilla Jan 31 '14 at 07:07
  • Use the Pythagorean theorem for a suitable right triangle. For the small circle, draw a line from the circle's center to the lower right vertex, and then drop a perpendicular from the circle's center to the right edge of the square. For the large circle, I leave it to you to find the appropriate triangle. Look at the equations. – heropup Jan 31 '14 at 07:07
  • Perhaps I'm asking in the wrong place @Martin, but saying elementary analytic geometry doesn't really help me here. Nor does the further explanation from heropup. I'm looking at the formulas, I've got a piece of scratch paper filled with attempts, and I can't even begin to comprehend how you've attempted this. Looking at answers like this I get the concept, but giving the equations without even explaining what they are pointing at is way over my head to the point I can't even understand if it's right or how this is the answer. – jmac Jan 31 '14 at 07:16
  • @jmac, read the explanation by heropup. – Martín-Blas Pérez Pinilla Jan 31 '14 at 07:19
  • Thanks for the image. I am still baffled as to how you are finding the center of the smaller circle in the first place. I can get to the center of the large circle, but the smaller circle I can't figure out how to get to the center of it as I can't figure out where the reference is. – jmac Jan 31 '14 at 07:29
  • I...I don't even know what to say. The diagram is symmetric. The center of the small circle lies somewhere on the (vertical) axis of symmetry. The point is, I don't know where it is yet. I'm solving for the radius $r$ of the circle. There's no coordinate system involved--the annotated picture I included shows you that, if the radius of the circle is $r$, then $r$ must satisfy the Pythagorean relationship I described earlier. I honestly cannot make it any simpler. – heropup Jan 31 '14 at 07:33
  • Okay so I just saw your annotated diagram, and that is NOT how you can get the radius of the small circle. You can get the large one that way, but only because of the fact that one point of tangency happens to be at the center of the square. – heropup Jan 31 '14 at 07:39
  • Okay, I think I am following you know. Apologies for being slow here. So the smaller circle is $r = x/8$, and the larger circle is $R = x/6$ all said and done. I understand the method now, I was being tripped up by the lack of a straight answer and my inability to do grade school algebra. No real geometry beyond the pythagorean theorem is required. That is disappointing. And I take it this is equally trivial? – jmac Jan 31 '14 at 07:51