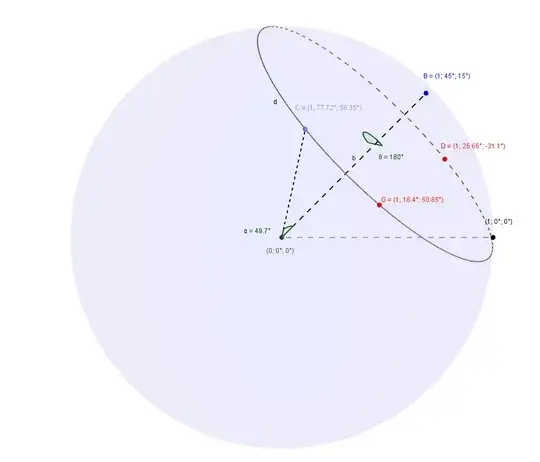
Construct a parametrization of the circle $d$ in $3$ stages of increasing generality.
1. Suppose that $B$ is the north pole (colatitude $\varphi = 0$).
The circle is the parallel (line of constant colatitude $\varphi = \alpha$), which has $z = \cos \alpha$ and $r = \sin \alpha$; hence, it is parametrized in rectangular coordinates by $t \mapsto \big( x(t), y(t), z(t) \big)$, where
$$
\left\{
\begin{align}
x &= \sin \alpha \cos t \\
y &= \sin \alpha \sin t \\
z &= \cos \alpha
\end{align}
\right.
\qquad \text{for } 0 \le t < 2\pi.
$$
2. Suppose that $B$ is on the prime meridian (longitude $\theta = 0$) but colatitude has some value $\varphi = \beta$, where $0 < \beta \le \pi$.
We take the coordinates $(x, y, z)$ of the circle with center at the north pole (from 1.) and rotate them through an angle $\beta$ along the great circle that includes the prime meridian. Using standard formulas for rotating coordinates, we have
$$
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
\mapsto
\begin{bmatrix}
x \cos \beta + z \sin \beta \\ y \\ -x \sin \beta + z \cos \beta
\end{bmatrix}.
$$
3. Suppose that $B$ is anywhere on the sphere with spherical coordinates $(\varphi, \theta) = (\beta, \gamma)$. Take the resulting coordinates from 2. and rotate them about the polar axis of the sphere through an angle of $\gamma$:
$$
\begin{bmatrix}
x \\ y \\ z
\end{bmatrix}
\mapsto
\begin{bmatrix}
x \cos \gamma - y \sin \gamma \\ x \sin \gamma + y \cos \gamma \\ z
\end{bmatrix}.
$$
Putting these together, the general case for a circle $d$ with center at $(\varphi, \theta) = (\beta, \gamma)$ and central angle $\alpha$ (that determines the radius) has rectangular coordinates:
$$
\left\{
\begin{align}
x &= \phantom{-}( \sin \alpha \cos \beta \cos \gamma ) \cos t + ( \sin \alpha \sin \gamma ) \sin t - (\cos \alpha \sin \beta \cos \gamma ) \\
y &= -( \sin \alpha \cos \beta \sin \gamma ) \cos t + ( \sin \alpha \cos \gamma ) \sin t + (\cos \alpha \sin \beta \sin \gamma ) \\
z &= \phantom{-}( \sin \alpha \sin \beta ) \cos t + \cos \alpha \cos \beta.
\end{align}
\right.
$$