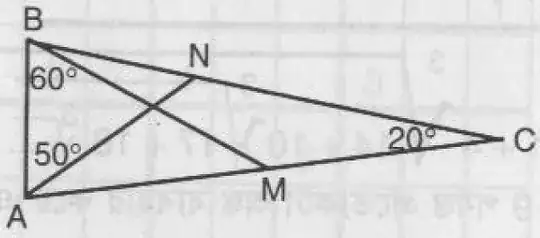
Here $\triangle ABC$ is a isosceles triangle with $AC=BC,\angle C=20^\circ$, $\angle ABM=60^\circ$ and $\angle BAN=50^\circ$. What is the value of $\angle BMN$? please help me with this problem.
Asked
Active
Viewed 342 times
2
-
There is no line from M to N. Are you sure this is what you want us to calculate? And if so, what have you tried? – recursive recursion Jan 12 '14 at 15:44
-
Do you mean $MBN$? – Jemmy Jan 12 '14 at 15:46
-
75.02492 degrees – GEdgar Apr 06 '15 at 14:49
1 Answers
2
The answer is $30^\circ$.
Proof: Take a point $F$ on $CB$ such that $BM=BF$. Also, take a point $G$ on $MF$ such that $CM=CG.$ (Note that $G$ is outside of $CBA$)
Since $$\angle{MFB}=\angle{BMF}=80^\circ,$$ we have $$\angle{GMC}=\angle{MFB}-\angle{MCF}=60^\circ.$$ Since $$\angle{GFC}=80^\circ=\angle BAM,$$ $$\angle{GCF}=40^\circ=\angle BMA,$$ $$\begin{align}CF&=CB-BF\\&=CB-BM\\&=CA-CM\\&=MA,\end{align}$$ we know that two triangles $CGF$ and $MBA$ are congruent.
Hence, $$\angle CGM=\angle MBA=60^\circ.$$ Hence, we know that a triangle $CGM$ is an equilateral triangle.
Hence, $$\begin{align}FN&=BF-BN\\&=BM-BA\\&=CM-FG\\&=GM-FG\\&=FM.\end{align}$$ Since, $$\angle NMF=\angle FNM=50^\circ,$$ we have $$\angle BMN=\angle BMF-\angle NMF=30^\circ.$$
mathlove
- 151,597
-
-
-
@pirsquare: Thanks for the catch. I needed to write a bit more. I edited them. – mathlove Apr 06 '15 at 13:01