7

The powers of the roots $\lambda$ of these polynomials $$p_n(x):=\sum_{k=1}^{n-1}\frac{n!}{(n-k)!}x^{k-1}$$ (compare with the $p_n$ here) sum to these values $$\sum_\lambda \lambda^k=-(-1)^k\frac{B_k}{k!} \textrm{for } k=1..n-2$$ The $B_k$ are the $k$th Bernoulli numbers $-\frac{1}{2}, \frac{1}{6}, 0, -\frac{1}{30}...$ Since $|\lambda|<1$ (fine to just assume) we have the geometric series $$\sum_{k=0}^\infty(\lambda x)^k=\frac{1}{1-\lambda x}$$ at least for $|x|\leq1$ but most of the $\lambda$ go to zero as $n$ increasesso the radius of convergence also may increase.

By summing over all $n-2$ roots $\lambda$ we get for the first $n-2$ terms of the left hand side. $$\sum_{k=1}^{n-2}(\lambda_1 x)^k+\sum_{k=1}^{n-2}(\lambda_2 x)^k+...=-\sum_{k=1}^{n-2}(-1)^kB_k\frac{x}{k!}^k$$ Which if you start at $k=0$ and go to $\infty$ converges to $-x/(1-\exp(-x))$ see here.

Question: Is $$-x/(1-\exp(-x))=\lim_{n\rightarrow \infty} \left (\sum_{p_n(\lambda)=0}\frac{1}{1-\lambda x}-n+1 \right)$$ at least for $|x|<1$? Here is a plot for $-x/(1-\exp(-x))$ (green) and $\sum_\lambda \frac{1}{1-\lambda x}-n+1$ (blue) for $n=16$

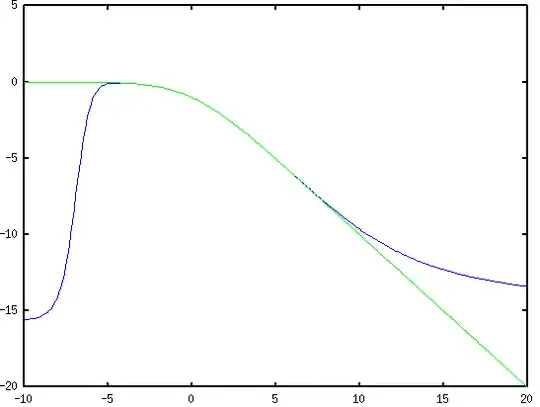
good fit for $|x|<1$

and the octave code to generate it

n = 16;

lambda = roots(factorial(n)./factorial(n - [n-1:-1:1]));

x = -10:1/10:20;

y = zeros(1,length(x));
for i = 1:length(x)
  y(i) = sum(1./(1-lambda*x(i)));
end

plot(x, y-n+1, 'b-', x, -x./(1-exp(-x)), 'g-')

axis([-10 +20 -20 +5])
Community
  • 1

1 Answers1

6

The desired limit formula holds for all real $x$, and even for all complex $x$ other than nonzero integer multiples of $2\pi i$.

The key is to write $\sum_{p_n(\lambda)=0} 1/(1-\lambda x)$ in terms of a logarithmic derivative.

We may assume $x\neq 0$. Define $$ q_n(x) = \frac{x^{n-1}}{n!} p_n(1/x) = \sum_{m=1}^{n-1} \frac{y^m}{m!} $$ (with $m=n-k$), so that $$ q_n(x) = x \prod_\lambda (1-\lambda x), $$ the product ranging over the $n-2$ zeros of $p_n$ (with multiplicity if necessary). Therefore $$ -x\frac{q'_n(x)}{q_n(x)} = -x \; \Bigl(\frac1x - \sum_\lambda \frac\lambda{1-\lambda x} \Bigr) = -1 + \sum_\lambda \frac{\lambda x}{1-\lambda x}. $$ Each summand $\frac{\lambda x}{1-\lambda x}$ can be written as $\frac1{1-\lambda x} - 1$, so the right-hand side is $$ \sum_\lambda \frac1{1-\lambda x} - n + 1. $$ On the left-hand side, $q'_n(x)$ is a partial sum of the power series for $e^x$, and $q_n(x)$ is a partial sum of the power series for $e^x-1$. These power series converge for all $x \in {\mathbb C}$. Therefore, as long as $e^x - 1 \neq 0$, $$ -x \frac{q'_n(x)}{q_n(x)} \rightarrow -x \frac{e^x}{e^x-1} = \frac{-x}{1-e^{-x}}, $$ and the proof is complete.

Noam D. Elkies
  • 26,275