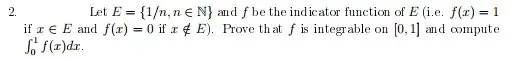
f is discontinuous on [0,1] so it's not integrable? but I think the answer is yes, it is integrable. But i dont know how to prove that.
any hint would be great. thanks
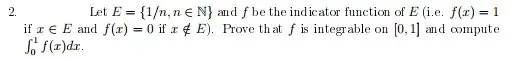
f is discontinuous on [0,1] so it's not integrable? but I think the answer is yes, it is integrable. But i dont know how to prove that.
any hint would be great. thanks
Notice that for any partition $\pi$, we have $L(f,\pi) = 0$, so we know what the result will be.
To directly show that $f$ is Riemann integrable, let $\epsilon>0$. We need to construct a partition. Let $0, \frac{1}{2} \epsilon$ be the first two points in the partition. Since $f \le 1$, we see that $\sup_{x \in [0, \frac{1}{2} \epsilon]} f(x) l([0, \frac{1}{2} \epsilon]) \le \frac{1}{2} \epsilon$.
Note that $E \cap (\frac{1}{2} \epsilon, 1]$ is finite, and let $p_1< p_2 < \cdots < p_n$ be the points. Choose the points $o_k,q_k$ so that $o_1 < p_1 < q_1 < o_2 < p_2 < q_2 < \cdots < o_n < p_n < q_n$ such that $q_k-o_k < \frac{1}{2n} \epsilon$, and note that $f(x) = 0$ for $ x \in (\frac{1}{2} \epsilon, 1] \cap ( \cup_k [o_k, q_k] )^c$.
Then with the partition $\pi=(0,\frac{1}{2} \epsilon, o_1 , p_1 , q_1 , o_2 , p_2 , q_2 , \cdots , o_n , p_n , q_n, 1)$, we see that $U(f,\pi) \le \frac{1}{2} \epsilon + n \frac{1}{2n} \epsilon = \epsilon$.
Hence $\inf_\pi U(f,\pi) = 0$. It follows that $\int_0^1 f(x) dx = 0$.
I assume you are talking about Riemann Integrability. The following result is useful to check the Riemann integrability of your function
A function $g(x)$ is Riemann integrable on $[a,b]$ iff
i) $g$ is bounded
ii) $g$ has a countable number of discontinuities (or it is discontinuous on a set of measure zero).