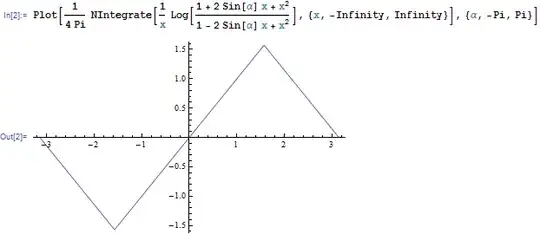Integral $\int_{-1}^{1} \frac{1}{x}\sqrt{\frac{1+x}{1-x}} \log \left( \frac{(r-1)x^{2} + sx + 1}{(r-1)x^{2} - sx + 1} \right) \, \mathrm dx$

Question

Regarding this problem, I conjectured that

$$ I(r, s) = \int_{-1}^{1} \frac{1}{x}\sqrt{\frac{1+x}{1-x}} \log \left( \frac{(r-1)x^{2} + sx + 1}{(r-1)x^{2} - sx + 1} \right) \, \mathrm dx = 4 \pi \operatorname{arccot} \sqrt{ \frac{2r + 2\sqrt{r^{2} - s^{2}}}{s^{2}} - 1}. $$

Though we may try the same technique as in the previous problem, now I'm curious if this generality leads us to a different (and possible a more elegant) proof.

Indeed, I observed that $I(r, 0) = 0$ and

$$\frac{\partial I}{\partial s}(r, s) = \int_{0}^{\infty} \left\{ \frac{2\sqrt{y}}{(r-s)y^{2} + 2(2-r)y + (r+s)}+\frac{2\sqrt{y}}{(r+s)y^{2}+ 2(2-r)y + (r-s)} \right\} \,\mathrm dy, $$

which can be evaluated using standard contour integration technique. But simplifying the residue and integrating them seems still daunting.

---

EDIT. By applying a series of change of variables, I noticed that the problem is equivalent to prove that

$$ \tilde{I}(\alpha, s) := \int_{-1}^{1} \frac{1}{x}\sqrt{\frac{1+x}{1-x}} \log \left( \frac{ 1 + 2sx \sin\alpha + (s^{2} - \cos^{2}\alpha) x^{2}}{ 1 - 2sx \sin\alpha + (s^{2} - \cos^{2}\alpha) x^{2}} \right) \, \mathrm dx = 4\pi \alpha $$

for $-\frac{\pi}{2} < \alpha < \frac{\pi}{2}$ and $s > 1$. (This is equivalent to the condition that the expression inside the logarithm is positive for all $x \in \Bbb{R}$.)

Another simple observation. once you prove that $\tilde{I}(\alpha, s)$ does not depend on the variable $s$ for $s > 1$, then by suitable limiting process it follows that

$$ \tilde{I}(\alpha, s) = \int_{-\infty}^{\infty} \log \left( \frac{ 1 + 2x \sin\alpha + x^{2}}{ 1 - 2x \sin\alpha + x^{2}} \right) \, \frac{\mathrm dx}{x}, $$

which (I guess) can be calculated by hand. The following graph may also help us understand the behavior of this integral.

Answer 1

So, following the procedure I outlined here, I get for the transformed integral:

$$I(r,s) = \int_0^{\infty} dv \frac{4 s \left(v^2-1\right) \left(v^4-(4 r-6) v^2+1\right)}{v^8+4 \left(2 r-s^2-1\right) v^6 +2 \left(8 r^2-8 r-4 s^2+3\right) v^4 +4 \left(2 r-s^2-1\right) v^2 +1} \log{v} $$

Note that this reduces to the integral in the original problem when $r=3$ and $s=2$. Then we see that the roots of the denominator satisfy the same symmetries as before, so we need only find one root of the form $\rho e^{i \theta}$ where

$$\rho = \sqrt{\frac{r+\sqrt{r^2-s^2}}{2}} + \sqrt{\frac{r+\sqrt{r^2-s^2}}{2}-1}$$

and

$$\theta = \arctan{\sqrt{\frac{2 \left (r+\sqrt{r^2-s^2}\right )}{s^2}-1}}$$

Using the same methodology I derived, I am able to confirm your conjecture.

Answer 2

Just for references, I remark that the following proposition was proved in my answer:

Proposition. If $0 < r < 1$ and $r < s$, then $$ I(r, s) := \int_{-1}^{1} \frac{1}{x} \sqrt{\frac{1+x}{1-x}} \log \left( \frac{1 + 2rsx + (r^{2} + s^{2} - 1)x^{2}}{1 - 2rsx + (r^{2} + s^{2} - 1)x^{2}} \right) \, dx = 4\pi \arcsin r. \tag{*} $$

Recently, I found an alternate proof which is much simpler and does not use contour integration technique.

Lemma 1. For any $k = 0, 1, 2, \cdots$ we have $$ \int_{0}^{1} \frac{x^{2k}}{\sqrt{1-x^{2}}} \, dx = (-1)^{k} \frac{\pi}{2} \binom{-1/2}{k}. $$

Since this is so famous, we skip the proof.

Lemma 2. For any $z \in \Bbb{C}$ with $|z| \leq 1$, we have $$ f(z) := - \int_{-1}^{1} \frac{1}{x} \sqrt{\frac{1+x}{1-x}} \log(1 - zx) \, dz= \pi \sin^{-1} z - \pi \log \left( \tfrac{1}{2}+\tfrac{1}{2}\sqrt{1-z^{2}} \right) . \tag{1} $$

Proof of Lemma. Expand $-\log(1-zx)$ using the MacLaurin series. Then we have

$$ f(z) = \sum_{n=1}^{\infty} \frac{z^{n}}{n} \int_{-1}^{1} x^{n-1} \sqrt{\frac{1+x}{1-x}} \, dx. \tag{2} $$

To identify the coefficient, we observe that

\begin{align*} \int_{-1}^{1} x^{n-1} \sqrt{\frac{1+x}{1-x}} \, dx &= \int_{0}^{1} x^{n-1} \sqrt{\frac{1+x}{1-x}} \, dx + \int_{-1}^{0} x^{n-1} \sqrt{\frac{1+x}{1-x}} \, dx \\ &= \int_{0}^{1} x^{n-1} \frac{(1+x) + (-1)^{n-1}(1-x)}{\sqrt{1-x^{2}}} \, dx \end{align*}

Dividing the cases based on the parity of $n$, it follows that

$$ \int_{-1}^{1} x^{n-1} \sqrt{\frac{1+x}{1-x}} \, dx = \begin{cases} \displaystyle 2\int_{0}^{1} \frac{x^{n}}{\sqrt{1-x^{2}}} \, dx, & n \text{ even} \\ \displaystyle 2\int_{0}^{1} \frac{x^{n-1}}{\sqrt{1-x^{2}}} \, dx, & n \text{ odd}. \end{cases}. $$

Thus by Lemma 1 we know an exact formula for the coefficients of $f(z)$ in $\text{(2)}$, and we obtain

\begin{align*} f(z) &= \pi \sum_{k=0}^{\infty} \binom{-1/2}{k} \frac{(-1)^{k} z^{2k+1}}{2k+1} + \pi \sum_{k=1}^{\infty} \binom{-1/2}{k} \frac{(-1)^{k} z^{2k}}{2k} \\ &= \pi \int_{0}^{z} \frac{dw}{\sqrt{1- w^{2}}} + \pi \int_{0}^{z} \left( \frac{1}{\sqrt{1- w^{2}}} - 1 \right) \, \frac{dw}{w}. \end{align*}

Therefore evaluating the last integral yields $\text{(1)}$ as desired. ////

Proof of Proposition. Now let us return to the proof of our proposition. Let $r = \cos\alpha$ and $s = \cos\beta$ for any $\alpha, \beta \in \Bbb{R}$. Then by a simple application of trigonometry, we find that

$$ 1 \pm 2rsx + (r^{2} + s^{2} - 1)x^{2} = (1 \pm x \cos(\alpha+\beta))(1 \pm x \cos(\alpha-\beta)). $$ So it follows that

\begin{align*} I(r, s) &= f(\cos(\alpha+\beta)) + f(\cos(\alpha-\beta)) - f(-\cos(\alpha+\beta)) - f(\cos(\alpha-\beta)) \\ &= 2\pi \sin^{-1}\cos(\alpha+\beta) + 2\pi \sin^{-1}\cos(\alpha-\beta). \end{align*}

If we restrict our attention to the case $0 < \alpha < \beta < \pi/2$, then it follows that we have

\begin{align*} I(r, s) &= 2\pi \sin^{-1}\cos(\alpha+\beta) + 2\pi \sin^{-1}\cos(\alpha-\beta) \\ &= 4\pi ( \tfrac{\pi}{2} - \alpha ) \\ &= 4\pi \arcsin r. \end{align*}

This completes the proof.

Answer 3

The integral can be generalized as $$ J(p, q) = \int_{-1}^{1} \frac{1}{x}\sqrt{\frac{1+x}{1-x}} \log \left( \frac{px^{2} + qx + 1}{px^{2} - qx + 1} \right) \, \mathrm dx. $$ Under the substitution x↦−x (inspired from Ivan) and adding the integrals one obtains $$ J(p,q)=\int_{-1}^{1} \frac{1}{x} \frac{1}{\sqrt{1-x^2}} \log \left( \frac{px^{2}+2qx+1}{px^{2}-2qx+1} \right) \, dx $$ The proof is just simply to use the same method I used in Integral $\int_{-1}^1\frac1x\sqrt{\frac{1+x}{1-x}}\ln\left(\frac{2\,x^2+2\,x+1}{2\,x^2-2\,x+1}\right) \mathrm dx$. Write $$ (ax+1)(bx+1)=px^2+2qx+1,(-ax+1)(-bx+1)=px^2-2qx+1 $$ where $$ a = q+\sqrt{q^2-p},b=q-\sqrt{q^2-p}$$ Under $x\to -x$, one has $$\begin{eqnarray} J(p,q) &=& \int_{-1}^{1} \frac{1}{x} \frac{1}{\sqrt{1-x^2}} \log \left( \frac{px^{2}+2qx+1}{px^2-2qx+1} \right) \, dx \\ &\overset{x\to\sin x}=&\int_{-\pi/2}^{\pi/2}\frac1{\sin x}\log\bigg(\frac{p\sin^2x+2q\sin x+1}{p\sin^2x-2q\sin x+1}\bigg) \, dx \\ &=&\int_{-\pi/2}^{\pi/2}\frac1{\sin x}\log\bigg(\frac{(a\sin x+1)(b\sin x+1}{(-a\sin x+1)(-b\sin x+1)}\bigg) \, dx \\ &=&\int_{-\pi/2}^{\pi/2}\bigg(\int_{-a}^a\frac1{t\sin x+1}\,dt+\int_{-b}^b\frac1{t\sin x+1}\,dt\bigg) \, dx \\ &=&\int_{-a}^a\int_{-\pi/2}^{\pi/2}\frac1{t\sin x+1}\,dx\,dt+\int_{-b}^b\int_{-\pi/2}^{\pi/2}\frac1{t\sin x+1}\,dx\,dt. \end{eqnarray}$$ Using $$ \int_{-\pi/2}^{\pi/2}\frac{1}{t\sin x+1}\ \mathrm dx=\frac{\pi}{\sqrt{1-t^2}} $$ one has $$ J(p,q)=\int_{-a}^a\frac{\pi}{\sqrt{1-t^2}}\,dt+\int_{-b}^b\frac{\pi}{\sqrt{1-t^2}}\,dt=2\pi(\arcsin(a)+\arcsin(b)). $$ If $0<r<s\le1$, let $r=\sin u,s=\sin v$ where $0<u<v<\frac{\pi}2$. Then $$ p=r^2+s^2-1=\sin^2v-\cos^2u,q=\sin u\sin v $$ and $$ a=\cos(u-v),b=-\cos(u+v). $$ It is easy to check $$ \sin(\arcsin(a)+\arcsin(b))=\sin(2u)$$ and hence $$ I(r,s)=2\pi\cdot 2u=4\pi\arcsin r $$ which is the desired result. For $0<r<1,s>1$, one can use the same way to handle.

Answer 4

$I$ can be simplified as

$$\require{cancel}\begin{align}I(r,s)&=2\int_0^1\ln\left(\frac{(r-1)x^2+sx+1}{(r-1)x^2-sx+1}\right)\frac{\mathrm dx}{x\sqrt{1-x^2}}\\&\overset{x\to\operatorname{sech}x}{=}2\int_0^\infty\ln\left(\frac{\cosh^2x+s\cosh x+r-1}{\cosh^2x-s\cosh x+r-1}\right)\mathrm dx\end{align}$$

Now, partially differentiating under the integral sign w.r.t $r$,

$$\begin{align}\frac{\partial I}{\partial r}&=2\int_0^\infty\frac{\mathrm dx}{\cosh^2x+s\cosh x+r-1}-2\int_0^\infty\frac{\mathrm dx}{\cosh^2x-s\cosh x+r-1}\\&=-4s\int_0^\infty\frac{\cosh x}{\cosh^4x+(2r-2-s^2)\cosh^2x+(r-1)^2}\mathrm dx\\&\overset{\sinh x\to x}{=}\cancelto0{\frac{2s}{\sqrt{r^2-s^2}}\int_0^\infty\frac{\mathrm d\left(x+\frac{\sqrt{r^2-s^2}}x\right)}{\left(x+\frac{\sqrt{r^2-s^2}}x\right)^2+2r-s^2-2\sqrt{r^2-s^2}}}-\frac{2s}{\sqrt{r^2-s^2}}\int_0^\infty\frac{\mathrm d\left(x-\frac{\sqrt{r^2-s^2}}x\right)}{\left(x-\frac{\sqrt{r^2-s^2}}x\right)^2+2r-s^2+2\sqrt{r^2-s^2}}\\&=\frac{-2\pi s}{\sqrt{r^2-s^2}\sqrt{2r-s^2+2\sqrt{r^2-s^2}}}\end{align}$$

Let $v=\sqrt{2r-s^2+2\sqrt{r^2-s^2}}$, then

$$\begin{align}v\frac{\partial v}{\partial r}&=\frac{\sqrt{r^2-s^2}+r}{\sqrt{r^2-s^2}}\\\implies\frac{2\partial v}{v^2+s^2}&=\frac{\partial r}{\sqrt{r^2-s^2}\sqrt{2r-s^2+2\sqrt{r^2-s^2}}}\\\implies\partial I&=\frac{-4\pi s}{v^2+s^2}\partial v\\\implies I(r,s)&=4\pi\cot^{-1}\sqrt{\frac{2r-s^2+2\sqrt{r^2-s^2}}{s^2}}\end{align}$$

The constant of integration above is zero since as $s\to0$, the argument in the arc-cotangent tends to infinity, so its arc-cotangent approaches zero and so does $I$.