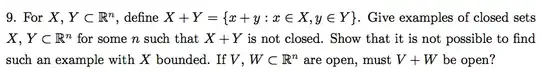
Ok so well Im struggling to find examples for the first two parts and for the last, well I don't think it is open but can't again find an example. Thanks.
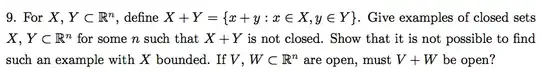
Ok so well Im struggling to find examples for the first two parts and for the last, well I don't think it is open but can't again find an example. Thanks.
Since the second question is not answered in the link I gave, I will put its answer here. If $X$ is closed and bounded then its compact by Heine Borel theorem. Let $x_n+y_n$ be a convergent sequence in $X+Y$. Since $X$ is compact, therefore $\{x_n\}$ has a convergent subsequence $\{x_{n_k}\}$ that converges to $x$. $x$ must lie in $X$ , because $X$ is closed. Since $x_n+y_n$ converges, therefore $x_{n_k}+y_{n_k}$ converges as well. Since $x_{n_k}$ converges and $x_{n_k}+y_{n_k}$ converges, therefore $y_{n_k}$ converges to a limit say $y$. $y$ must lie in $Y$, because $Y$ is closed. Therefore the limit of $x_n+y_n$ which is $x+y$ must be inside $X+Y$, because $x\in X$,$y\in Y$