Behavior of a system of differential equations after a long time

Question

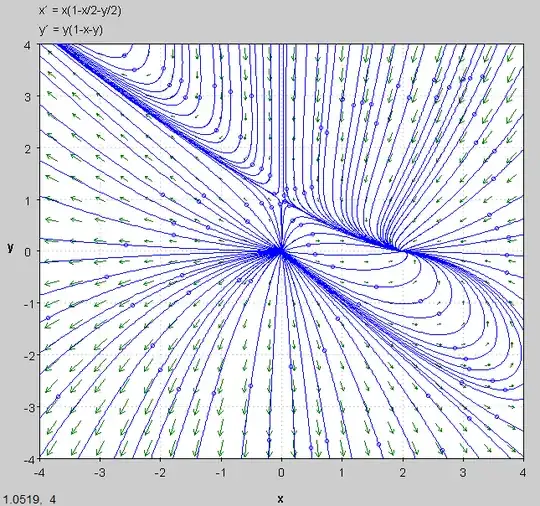
I am looking at two systems of differential equations:

$$ \frac{1}{x} \frac{dx}{dt} = 1 - \frac{x}{2} - \frac{y}{2} $$ $$ \frac{1}{y} \frac{dy}{dt} = 1 - x - y $$ $$ x(0)=1, y(0)=3.5 $$

How would one figure out the behavior of this system as time approaches infinity? Do you need to use a calculator?

haven't looked at it very much but you can assume x > 0 and y > 0 (since there is the 1/x and 1/y) and do 2 * equation 1 - equation 2 to get a first relation between x and y — Thomas, Nov 10 '13 at 20:27
You should look at concepts of stability, and for phase portraits you need a calculator. — Ömer, Nov 10 '13 at 20:44
I'm not sure how to enter this into a calculator in dy/dx form. — Bob Shannon, Nov 10 '13 at 21:06
I don't mean hand calculator by calculator, i mean a CAS such as Maple, Mathematica,...even there are online sites that you can plot phase portraits, i also recommend you to look at here http://math.stackexchange.com/questions/457102/stability-of-nonlinear-system-with-borderline-linearization/457329#457329 and — Ömer, Nov 10 '13 at 21:38

Amzoti · Accepted Answer · 2013-11-10T21:52:14.263

2

You have two options:

(1) Use a numerical scheme (are you currently working on those)
(2) Plot a phase portrait and look at the behavior for that initial condition. In this case you can find the critical points and analyze them.

Here is the phase portrait (notice the long term behavior is broken into stable and unstable regions):

enter image description here

edited Nov 10 '13 at 21:52

answered Nov 10 '13 at 21:45

Amzoti

This is exactly what I was looking for. The phase portrait makes it so easy -- y clearly tends to zero and x tends to 2 as t approaches infinity. I need to learn how to use Maple or similar for stuff like this. – Bob Shannon Nov 11 '13 at 00:56
Nice phase portrait, once again! – amWhy Nov 11 '13 at 01:53
@amWhy: Thanks, hope you Sunday is spectacular! – Amzoti Nov 11 '13 at 02:00

score 0 · Answer 2 · answered Nov 10 '13 at 20:28

0

You need to transform the system to the Laplace domain, then use the final value theorem: http://en.wikipedia.org/wiki/Final_value_theorem

answered Nov 10 '13 at 20:28

score 0 · Answer 3 · answered Nov 10 '13 at 21:43

0

What level is the question being asked at? It may be as simple as you are allowed to assume $dx/dt$ and $dy/dt$ tend to $0$ as $t\rightarrow \infty$.

answered Nov 10 '13 at 21:43

Matt Rigby

3 Answers3