Question:
Let $f: [a,\infty) \to \Bbb R \in C^2$ and the two following integrals converge: $$\int _a^\infty (f''(x))^2\,dx ,~~~~~~~~~ \int _a^\infty (f(x))^2\,dx$$
Prove that $\int _a^\infty (f'(x)^2)\,dx$ converges as well.
What we tried: Taylor expansion, Lagrange mean value theorem, integration by parts, comparison test, limit comparison test, none really helped us get there...
Hint 1: Integration by parts gives $$ \begin{align} \int_a^\infty f'(x)^2\,\mathrm{d}x &=\int_a^\infty f'(x)\,\mathrm{d}f(x)\\ &=\lim_{b\to\infty}f'(b)f(b)-f'(a)f(a)-\int_a^\infty f(x)f''(x)\,\mathrm{d}x\tag{1} \end{align} $$ Hint 2: As Giraffe points out, if $\int_a^\infty f'(x)^2\,\mathrm{d}x$ diverges, then by $(1)$, $\lim\limits_{x\to\infty}f'(x)f(x)=\infty$. Since $$ f(b)^2=\int_a^bf'(x)f(x)\,\mathrm{d}x\tag{2} $$ we get that $\int_a^\infty f(x)^2\,\mathrm{d}x$ diverges.
By the comments, this seems to be a bit more involved than befits a hint, so I will explain in more detail. Note that what follows is not needed due to Hint 2, but the ideas used are more generally applicable, so I will leave it.
Claim 1: $\displaystyle\lim_{x\to\infty}f'(x)=0$
Proof: Suppose not; then, for some $\epsilon\gt0$ and all $x_0$, there is an $x\ge x_0$ so that $|f'(x)|\ge\epsilon$.
Since $\|f''\|_{L^2}\lt\infty$, we can choose a $b$ so that $$ \int_b^\infty f''(x)^2\,\mathrm{d}x\le\epsilon^4\tag{1} $$ Then, for any $x,y\ge b$ so that $|x-y|\le1$, Cauchy-Schwarz says $$ \begin{align} |f'(x)-f'(y)| &\le\int_x^y|f''(x)|\,\mathrm{d}x\\ &\le\left(\int_x^y|f''(x)|^2\,\mathrm{d}x\right)^{1/2}|x-y|^{1/2}\\[9pt] &\le\epsilon^2\tag{2} \end{align} $$ For any $x_0\ge b+1$, we can choose an $x\ge x_0$ so that $|f'(x)|\ge\epsilon$. If $f'(x)$ and $f(x)$ have the same sign, let $I=[x,x+1]$, otherwise, let $I=[x-1,x]$.
$\hspace{2cm}$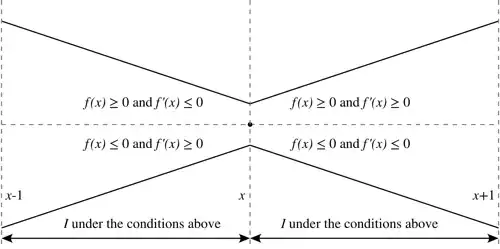
By $(2)$, for $t\in I$, $|f'(t)|\ge\epsilon-\epsilon^2$ and $|f(t)|\ge\left(\epsilon-\epsilon^2\right)|t-x|$. Thus, $$ \int_If(x)^2\,\mathrm{d}x\ge\frac13\left(\epsilon-\epsilon^2\right)^2\tag{3} $$ By supposition, we can find infinitely many points so that $|f'(x)|\ge\epsilon$. Therefore, $$ \int_b^\infty f(x)^2\,\mathrm{d}x\quad\text{diverges}\tag{4} $$ giving us a contradiction. QED
Claim 2: $\displaystyle\lim_{x\to\infty}f(x)=0$
Proof: Suppose not; then, for some $\epsilon\gt0$ and all $x_0$, there is an $x\ge x_0$ so that $|f(x)|\ge\epsilon$.
Since $\displaystyle\lim_{x\to\infty}f'(x)=0$, we can choose a $b$ so that for all $x\ge b$, $$ |f'(x)|\le\epsilon^2\tag{5} $$ Then, for any $x,y\ge b$ so that $|x-y|\le1$, the Mean-Value Theorem says $$ \begin{align} |f(x)-f(y)| &\le\max_{t\in[x,y]}|f'(t)||x-y|\\ &\le\epsilon^2\tag{6} \end{align} $$ For any $x_0\ge b+1$, we can choose an $x\ge x_0$ so that $|f(x)|\ge\epsilon$. For any $t\in[x-1,x+1]$, $|f(t)|\ge\epsilon-\epsilon^2$. Thus, $$ \int_{x-1}^{x+1}f(t)^2\,\mathrm{d}t\ge2\left(\epsilon-\epsilon^2\right)^2\tag{7} $$ By supposition, we can find infinitely many points so that $|f(x)|\ge\epsilon$. Therefore, $$ \int_b^\infty f(x)^2\,\mathrm{d}x\quad\text{diverges}\tag{8} $$ giving us a contradiction. QED
By Taylor's expansion with integral form of the remainder, $$f(x+1)=f(x)+f'(x)+g(x),\tag{1}$$ where $$g(x)=\int_x^{x+1}(x+1-t)f''(t)~dt.\tag{2}$$ By $(1)$, Minkowski's inequality and $\int_a^\infty (f(x))^2dx<\infty$, to show $\int_a^\infty (f'(x))^2dx<\infty$, it suffices to show that $$\int_a^\infty (g(x))^2dx<\infty.\tag{3}$$ By $(2)$ and Cauchy-Schwarz inequality, $$(g(x))^2\le \int_x^{x+1}(x+1-t)^2dt\cdot \int_x^{x+1}(f''(t))^2dt=\frac{1}{3}\int_x^{x+1}(f''(t))^2dt.\tag{4}$$ By $(4)$, Fubini's theorem and $\int_a^\infty (f''(x))^2dx<\infty$, $$3\int_a^\infty (g(x))^2dx\le\int_a^\infty\left(\int_x^{x+1}(f''(t))^2dt\right)dx\le \int_a^\infty\left(\int_{t-1}^tdx\right)(f''(t))^2dt<\infty,$$ which completes the proof of $(3)$.
This solution is quite unsatisfactory to me for its seemingly unnecessary complexity, but I post it anyway.
We introduce two lemmas
Lemma 1. Assume $g(x) : [a, \infty) \to \Bbb{R}$ is absolutely integrable and continuous. Then $$ \lim_{s \to 0^{+}} \int_{a}^{\infty} g(x)e^{-sx} \, dx = \int_{a}^{\infty} g(x) \, dx. $$
and
Lemma 2. Assume $g(x) : [a, \infty) \to \Bbb{R}$ is non-negative and continuous. Then regardless of the convergence of the integral, $$ \lim_{s \to 0^{+}} \int_{a}^{\infty} g(x)e^{-sx} \, dx = \int_{a}^{\infty} g(x) \, dx. $$
By integrating by parts,
\begin{align*} \int_{a}^{R} \{ f'(x) \}^{2} e^{-sx} \, dx &= \Big[ f(x)f'(x)e^{-sx} \Big]_{a}^{R} - \int_{a}^{R} f(x)f''(x) e^{-sx} \, dx \\ &\quad + \left[ \frac{s}{2} f(x)^{2} e^{-sx} \right]_{a}^{R} + \frac{s^{2}}{2} \int_{a}^{R} f(x)^{2} e^{-sx} \, dx. \end{align*}
From CS-inequality,
$$ |f'(x)| \leq |f'(a)| + \left| \int_{a}^{x} f''(t) \, dt \right| \leq |f'(a)| + \sqrt{x - a} \left( \int_{a}^{\infty} f''(t)^{2} \, dt \right)^{1/2} $$
and hence both $f$ and $f'$ are of polynomial growth. So taking $R \to \infty$,
\begin{align*} \int_{a}^{\infty} \{ f'(x) \}^{2} e^{-sx} \, dx &= - f(a)f'(a)e^{-sa} - \int_{a}^{\infty} f(x)f''(x) e^{-sx} \, dx \\ &\quad - \frac{s}{2} f(a)^{2} e^{-sa} + \frac{s^{2}}{2} \int_{a}^{\infty} f(x)^{2} e^{-sx} \, dx. \end{align*}
Taking $s \to 0^{+}$, Lemma 1 and 2 show that
\begin{align*} \int_{a}^{\infty} \{ f'(x) \}^{2} \, dx = - f(a)f'(a)- \int_{a}^{\infty} f(x)f''(x) \, dx. \end{align*}
Since the right-hand side is finite, the same is true for the left-hand side and the proof is complete.
Addendum. (Proof of Lemmas)
Proof of Lemma 1. For any $\epsilon > 0$, choose $R$ such that $\int_{R}^{\infty} |g(x)| \, dx < \epsilon$. Since $g(x)e^{-sx}$ is also absolutely integrable, its integral is well-defined and $$ \left| \int_{a}^{R} g(x)(1 - e^{-sx}) \, dx \right| \leq \int_{a}^{R} |g(x)| (1 - e^{-sx}) \, dx + \epsilon. $$ Taking $\limsup$ as $s \to 0^{+}$, followed by $\epsilon \to 0$, we obtain the desired result. ////
and
Proof of Lemma 2. Let $I$ denote the integral on the right-hand side and $J$ denote the limit of the left-hand side. On the one hand, from the following inequality $$ \int_{a}^{\infty} g(x)e^{-sx} \, dx \leq \int_{a}^{\infty} g(x) \, dx, $$ we have $J \leq I$. On the other hand, for each fixed $R > a$ we have $$ \int_{a}^{R} g(x) \, dx = \lim_{s\to 0^{+}} \int_{a}^{R} g(x)e^{-sx} \, dx \leq J. $$ Thus taking $R \to \infty$ we obtain $I \leq J$ and the equality follows. ////
