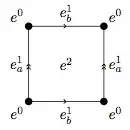
Homology of a torus

Question

I am trying to compute the homology of a torus by its chain map, rather than its equivalence to $\oplus H_n (S^1)$.

The post Homology groups of torus has been really helpful, but my question is, how can I come up with the boundary maps, so that I could use $H_n = \frac{\ker \partial_n}{\operatorname{Im} \partial_{n+1}}$?

The boundary map in the post you linked use cell homology. Did you learn how the boundary map is defined in that case? — , Nov 10 '13 at 08:54

score 3 · Accepted Answer · answered Nov 10 '13 at 20:33

3

The torus can be seen as

torus

with the left and right edges identified and the top and bottom edges identified, using the notation in the question linked to.

From this, you can compute the boundary maps: $\delta_2(e^2) = e^1_a + e^1_b - e^1_a - e^1_b = 0$, $\delta_1(e^1_a) = e^0 - e^0 = 0$, and $\delta_1(e^1_b) = e^0 - e^0 = 0$.

answered Nov 10 '13 at 20:33

Magdiragdag

15,435

That makes so much sense! It's so clear!! Thank you Magdiragdag! – 1LiterTears Nov 13 '13 at 02:46

Homology of a torus

1 Answers1