2

I know how to do Newton's method to find roots for a single variable function but then I got this problem and I am unsure of how to find the roots for multivariate functions using Newton's method:

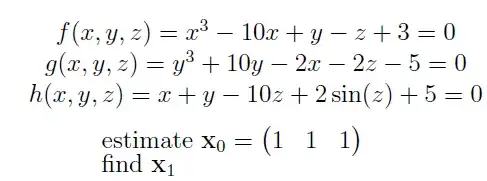
enter image description here

Narasimham
  • 42,260
Raynos
  • 1,673
  • http://math.stackexchange.com/questions/466809/solving-a-set-of-equations-with-newton-raphson – Amzoti Nov 08 '13 at 16:51
  • Thank you. I already have the 3 x 3 jacobian matrix and then I wasn't sure what to do. Ill read that post and hopefully get the steps to solve this. – Raynos Nov 08 '13 at 17:19
  • I can look at it later since I wrote what is in that post if you have issues. Also,, you only need to do one time step, so that is not bad. Regards – Amzoti Nov 08 '13 at 17:36

1 Answers1

-1

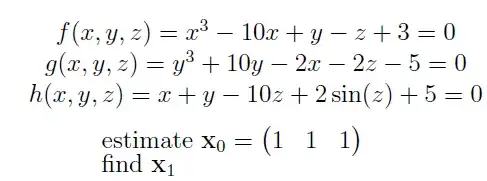
Say you put this on an spreadsheet:

  1. create a set (3 Rows 1 Column) of guesses for x, y, z; use 1 for each as specified in prob statement.

1

1

1

  1. Create a 3x1 set of function values each evaluated with the current guesses for x, y, and z

f(x,y,z)

g(x,y,z)

h(x,y,z)

  1. Create the 3x3 Jacobian Matrix. 1st row's three terms are the partial derivatives of the 1st equation with respect to x then y and then z. Etc for g(x,y,z) and h(x,y,z) for rows 2 and 3. These 9 terms are all evaluated using the current guessed values.

  2. Use the MInverse function in Excel to find the inverse of the 3x3 Jacobian (a 3x3). Call result J^-1. Note: when entering a matrix function, select the 3x3, enter equation into active cell, hit Shift-Enter-Return to create the matrix results. The equations will appear in braces; {.. }'s in the formula bar.

  3. Use the MMult function to multiply the J^1 3x3 matrix times the 3x1 matrix array of function values created in #2.

  4. The new values of x,y,z are the matrix of the x,y,z values created in #1 minus the result from #5. You will not need a matrix function since each value may be subtracted piece wise: x2 = x1 - first term from #5, etc.

  5. Repeat process starting at #1 but use new values for x,y,z calculated in #6 until convergence is satisfactory.

Note: non-linear systems can have multiple roots so the set you find depends on your initial guesses.

Saying it with mathematical succinctness, where X is an array of variables and f(X) an array of function values, repeating

X(i+1)=X(i)-J^-1 * f(X(i))

where J^-1 is the Jacobian of f(X(i))

will converge on X such that f(X) --> 0.

Stanley Howard
  • 1