3

Coxeter and Greitzer, in their excellent Geometry Revisited, list a few "hardy perennials" in elementary geometry: tough problems solvable by elementary methods. Their problem number 4 (on page 26 in my edition) is as follows:

Let $ABC$ be an isosceles triangle with equal angles $80^\circ$ at $B$ and $C$. Segments $BD$ and $CE$, extended to the opposite sides of the triangle, divide $\angle B$ and $\angle C$ into $60^\circ$/$20^\circ$ and $30^\circ$/$50^\circ$, respectively. (See figure below.) What is the measure of $\angle EDB$?

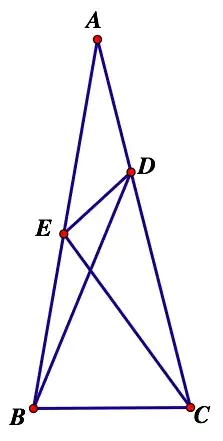
This site poses a similar problem, and calls it the "world's hardest easy geometry problem." In this problem, the $80^\circ$ angles are divided as $60^\circ$/$20^\circ$ and $70^\circ$/$10^\circ$.

Both of these problems are difficult and quite satisfying. (I will not give the answer here so as not to deprive casual searchers of the pleasure of solving them themselves; solutions to both can be easily found online.) I have also solved the related problem where the two $80^\circ$ angles are split as $70^\circ$/$10^\circ$ and $50^\circ$/$30^\circ$.

I have two questions:

  1. My solutions to all three problems have a similar flavor, but they're quite different. Is there a unifying insight or more sophisticated perspective that provides the solution to all three?

  2. All three problems are very pleasantly challenging, despite their apparent simplicity. What accounts for their difficulty? Is there a unifying insight that shows why precisely they are both difficult and solvable by elementary means?

Alf
  • 2,647
  • 1
    You will probably get better answers if you provide the solutions you want to compare and generalize. As it stands, anyone who wants to help must first solve three tricky problems, which might dissuade otherwise smart and helpful people who must allocate their time efficiency. – Potato Nov 03 '13 at 04:51
  • I'm not understanding the problem. Is the question whether $\angle EBD$ is $60^\circ$ or $20^\circ$? – dfeuer Nov 03 '13 at 04:53
  • I'm not sure what angle is being asked for here the way you specified it. When I read $\angle EBD$, I'm used to the middle letter being the vertex and the angle running counter-clockwise from a ray to the first letter to a ray to the third letter, which I believe is standard. Given that, can you specify again which angle you want? – David H Nov 03 '13 at 04:54
  • 1
    It should be $\angle EDB$ according to the link. – Potato Nov 03 '13 at 04:55
  • My apologies, the angle should be $\angle EDB$. Fixed. – Alf Nov 03 '13 at 14:10
  • Several of these result in looking at the $18-$gon, of which $ABC$ is a wedge. The lines $DE$ could result from connecting 2 other vertices, and after you identify why 2, the angle calculation is much simpler. – Calvin Lin Nov 03 '13 at 16:28

0 Answers0