My book gives a few definitions/formulas for obtaining linear approximation, but I'm having trouble understanding how to use them.
Heres the question:
a.) Use the Linear Approximation for f(x) = ln($x^2$ +3) at a = 1 with $\Delta x$ = 0.7 to approximate $\Delta f \approx$ ______________
b.) That Linear Approximation to the value of f(a + $\Delta x$) has error __________ (use calculator to get decimal value)
c.)That Linear Approximation in f(a + $\Delta x$) has percentage error __________
My book says something like this: $\Delta f$ = f(a + $\Delta x$) - f(a), where $\Delta x$ is small. By definition the derivative is the limit.
f '(a) = $\frac{lim}{\Delta x\rightarrow0}\Delta f$ = $\frac{lim}{\Delta x\rightarrow0}(\frac{f(a + \Delta x) - f(a)}{\Delta x})$ = $\frac{lim}{\Delta x\rightarrow0}\frac{\Delta f}{\Delta x}$ So when $\Delta x$ is small, we have $\frac{\Delta f}{\Delta x}\approx$ f '(a) and thus, $\Delta f \approx$ f '(a) $\Delta x$
I thought I was applying the formula correctly, but I guess not. Here's what I've done:
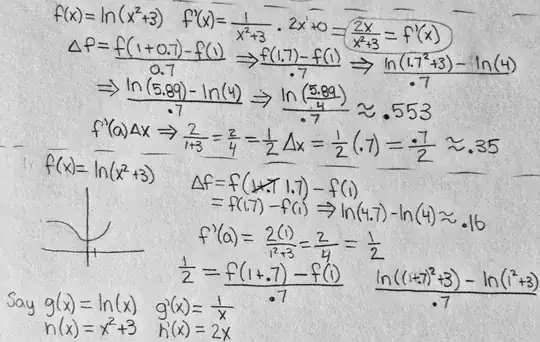
Can someone please help me out with solving this 3 part question? Thanks.