What is the proximal operator of the $ \left\| x \right\|_{\infty} $ norm:
$$ \operatorname{Prox}_{\lambda \left\| \cdot \right\|_{\infty}} \left( v \right) = \arg \min_{x} \frac{1}{2} \left\| x - v \right\|_{2}^{2} + \lambda \left\| x \right\|_{\infty} $$
I know we have to take the subgradient and compute it but I am a bit stuck.
Can anyone show me steps?
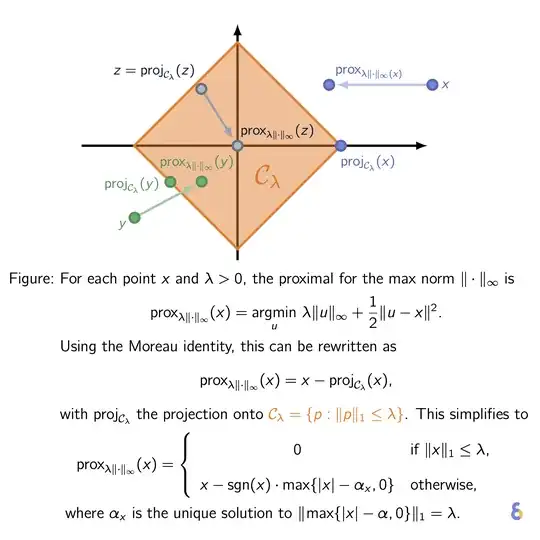
If you want to find the proximal operator of $\|x\|_{\infty}$, you don't want to compute the subgradient directly. Rather, as the previous answer mentioned, we can use Moreau decomposition: $$ v = \textrm{prox}_{f}(v) + \textrm{prox}_{f^*}(v)$$ where $f^*$ is the convex conjugate, given by: $$ f^*(x) = \underset{y}{\sup}\;(x^Ty - f(y))$$
In the case of norms, the convex conjugate is an indicator function based on the dual norm, i.e. if $f(x) = \|x\|_p$, for $p \geq 1$, then $f^*(x) = 1_{\{\|x\|_q \leq 1\}}(x)$, where $1/p + 1/q = 1$, and the indicator function is:
\begin{equation} 1_S(x)=\begin{cases} 0, & \text{if $x \in S$}.\\ \infty, & \text{if $x \notin S$}. \end{cases} \end{equation}
For your particular question, $f(x) = \|x\|_{\infty}$, so $f^*(x) = 1_{\{\|x\|_1\leq 1\}}(x)$.
We know $$\textrm{prox}_{f}(x) = x - \textrm{prox}_{f^*}(x)$$
Thus we need to find $$\textrm{prox}_{f^*}(x) = \underset{z}{\arg\min} \; \left(1_{\{\|z\|_1 \leq 1\}} + \|z - x\|_2^2 \right)$$
But this is simply projection onto the $L_1$ ball, thus the prox of the infinity norm is given by: $$ \textrm{prox}_{\|\cdot\|_{\infty}}(x) = x - \textrm{Proj}_{\{\|\cdot\|_1 \leq 1\}}(x)$$
The best reference for this is Neal Parikh, Stephen Boyd - Proximal Algorithms.
$$ \operatorname{prox}{ \lambda {\left| \cdot \right|}{\infty}} \left( x \right) = x - \lambda \operatorname{Proj}_{ \left{ \left| \cdot \right|_1 \leq 1 \right} }( \frac{x}{\lambda} ) $$
– Royi Mar 20 '20 at 16:51Let $f(x) = \|x\|_{\infty}$, so $f^*$ is the indicator function of $B$, where $B$ is the 1-norm unit ball.
The Moreau decomposition expresses the prox operator of $f$ in terms of the prox operator of $f^*$, which simply projects onto $B$. So we need to know how to project onto $B$. This is explained in ch. 8 ("the proximal mapping") of Vandenberghe's 236c notes. See slide 8-15 here.
As others noted, the proximal for the $\ell_\infty$ norm can here be deduced using the Moreau identity and dual norms. Note the dual norm of $\|\cdot\|_\infty$ is $\|\cdot\|_1$. In this case, we have \begin{align*} \mbox{prox}_{\lambda \|\cdot\|_\infty}(x) & = x - \lambda\cdot \mbox{prox}_{\lambda^{-1}\|\cdot\|_\infty^\star}\left(\frac{x}{\lambda}\right)\\ & = x - \lambda\cdot \mbox{proj}_{\|\cdot\|_1 \leq 1}\left(\frac{x}{\lambda}\right), \end{align*} where $\|\cdot\|_\infty^\star = \delta_{\|\cdot\|_1 \leq 1}(z)$. That is, the dual function $\|\cdot\|_\infty^\star$ is an indicator function (denoted here with $\delta$) which has value 0 inside the unit ball with respect to the $\ell_1$ norm and value $\infty$ elsewhere. The proximal for an indicator function is simply the projection onto the set, which is why the second equality holds. (This result can be found in Example 6.47 of Beck's First-Order Optimization Methods.)
This can be further simplified. Letting $u = \lambda z$, note \begin{align*} \mbox{proj}_{\|\cdot\|_1\leq 1}\left(\frac{x}{\lambda}\right) & = \underset{\|z\|_1\leq 1}{\mbox{argmin}} \frac{1}{2} \left\| z - \frac{x}{\lambda}\right\|^2 \\ & = \frac{1}{\lambda} \cdot \underset{\| u / \lambda\|_1\leq 1}{\mbox{argmin}}\ \frac{1}{2}\left\| \frac{u}{\lambda} - \frac{x}{\lambda}\right\|^2 \\ & = \frac{1}{\lambda} \underset{\|u\|_1\leq \lambda}{\mbox{argmin}}\ \frac{1}{2} \|u - x\|^2 \\ & = \frac{1}{\lambda} \cdot \mbox{proj}_{\|\cdot\|_1\leq\lambda} (x). \end{align*} Thus, \begin{equation*} \mbox{prox}_{\lambda \|\cdot\|_\infty}(x) = x - \mbox{proj}_{\|\cdot\|_1\leq\lambda}(x). \end{equation*} All that remains is to unpack the projection onto the $\ell_1$ ball of radius $\lambda$. From Theorem 6.30 and Example 6.33 in Beck's book, we have \begin{align*} \mbox{proj}_{\|\cdot\|_1\leq \lambda}(x) = \begin{cases}\begin{array}{cl} x & \mbox{if}\ \|x\|_1 \leq \lambda \\ \mbox{prox}_{\alpha_x \|\cdot\|_1}(x) & \mbox{otherwise}, \end{array}\end{cases} \end{align*} where $\alpha_x$ is a positive solution to \begin{equation*} \|\mbox{prox}_{\alpha \|\cdot\|_1}(x)\|_1 = \lambda. \end{equation*} Note here \begin{equation*} \mbox{prox}_{\alpha\|\cdot\|_1}(x) = \mbox{shrink}(x,\ \alpha) = \mbox{sgn}(x) \cdot \max\{ |x| - \alpha, 0\}, \end{equation*} where the absolute values and multiplication are applied element-wise. Putting everything together, this is summarized in the graphic below, which also shows 3 different cases for the $\ell_\infty$ proximal. (Note $\alpha_x$ can be computed, for example, using the bisection method.)
