Approximate the integral $\int_0^\pi \sin(x^3)\mathrm{d}x$ with a standard pocket calculator

Question

I came over the following integral $$ \int_0^\pi \sin(x^3) \mathrm{d}x $$ when a friend of mine tried to approximate it. The most obvious way is to use Taylor's formula, and then turn the integral into a sum. Eg $$ \int_0^\pi \sin(x^3) \mathrm{d}x \approx \sum_{k=0}^N \frac{1}{2} \frac{(-1)^k \pi^{3k+2}}{(3k+2)(2k+1)!} $$ The problem is the nominator increases much more rapidly than the denominator for the first 30 terms or so. Much faster than what a standard calculator can deal with. This can be seen here https://i.sstatic.net/O8aX0.jpg

By using the midpoint rule instead, the sum turns into $$ \int_0^\pi \sin(x^3) \mathrm{d}x \approx \frac{\pi}{2}\sum_{k=0}^N f\left( \frac{\pi}{2} \frac{2k-1}{N}\right) $$ Which converges to two decimal places in $36$ iterations, however to obtain a higher accuracy the convergence is slower than the Taylor series.

As a final note I also tried using the substitution $u \mapsto u^3$, but the series expansion did not improve.

My question is as follows: What is the least terms needed to approximate the integral to $3$ digits accuracy under the restrictions of using a standard pocket calculator?

To clearify the calculator does not have more than 8 digits accuracy, and can use sine and cosine. Oh, I also tried Simpsons that did not improve the convergence. Could Romberg, or Gaussian lead to faster convergence?

Answer 1

Here's a different flavor of approximation that's much more efficient: Expanding the integral in a series at $M = \infty$ (see below for the derivation) gives $$\int_0^M \sin(x^3) \,dx = \frac16 \Gamma\left(\frac13\right) - \frac1{3 M^2} \cos (M^3) + \cdots ,$$ where $\cdots$ denotes a remainder decaying as $O(M^{-5})$. Already for $M = \pi$ truncating after the first nonconstant term gives an absolute error $<10^{-3}$: \begin{align} \int_0^\pi \sin(x^3) \,dx &= \color{#007f00}{0.4158338146\ldots} \\ \frac16 \Gamma\left(\frac13\right) - \frac1{3 \pi^2} \cos (\pi^3) &= \color{#007f00}{0.415}5104547\ldots . \end{align}

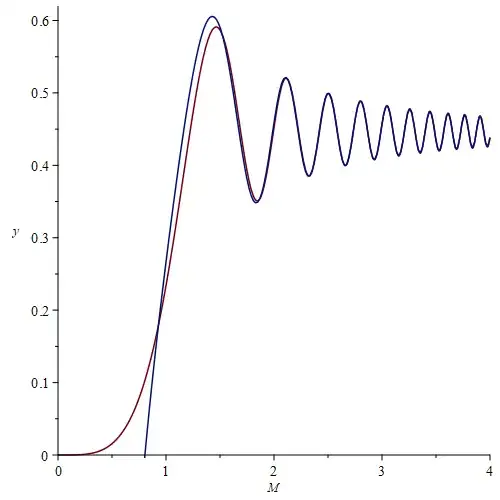
Figure 1. Graphs of $\color{#7f0000}{\int_0^M \sin (x^3) \,dx}$ (red) and the approximation $\color{#00007f}{\frac16 \Gamma\left(\frac13\right) - \frac1{3 M^2} \cos (M^3)}$ (blue):

This computation reduces the problem to evaluating or looking up $\operatorname{\Gamma}\left(\frac13\right) = 2.6789385347\ldots$ to adequate accuracy. This can be accomplished, e.g., with the approximation https://dlmf.nist.gov/5.11#E14, a truncation of which gives $$\operatorname{\Gamma}\left(\frac13\right) \approx \frac{6!}{\frac13 \cdot \frac43 \cdot \cdots \cdot \frac{16}3 \cdot \frac{19}3} \left(7 + \frac{\frac13 - 1}{2}\right)^{\frac13} = \frac1{1729}\left(\frac{3^{26} 5}{2^7}\right)^{\frac13} = \color{#007f00}{2.678}1972464\ldots ,$$ or a method of Borwein and Zucker, giving (where $m = \frac{2 - \sqrt 3}{4}$) $$\operatorname{\Gamma}\left(\frac13\right) = \frac{2^{\frac49} \pi^{\frac23}}{3^{\frac1{12}} \operatorname{AGM}\left(1, \sqrt{1 - m}\right)} \approx \frac{2^{\frac49} \pi^{\frac23}}{3^{\frac1{12}} (1 - m)^{\frac14}} = \frac{2^{\frac{25}{36}} \pi^{\frac23}}{3^{\frac1{12}} (1 + \sqrt{3})^{\frac16}} = \color{#007f00}{2.67}90056121\ldots ,$$ either of which would contribute $< 10^{-4}$ to the error in the approximation of $\int_0^\pi \sin(x^3) \,dx$. See answers to this question for more details of both of these approximations. Alternatively, since $e^{-u^3}$ decays rapidly enough, we have $$\Gamma\left(\frac13\right) = 3\int_0^\infty e^{-u^3} \,du \approx 3 \int_0^2 e^{-u^3} \,du,$$ and already for $n = 3$ Simpson's rule gives $\color{#007f00}{2.67}98249579\ldots$, an absolute error $< 10^{-3}$ ($n = 5$ gives an absolute error $< 10^{-4}$).

---

To establish the above terms of the series (and the decay of the remainder term), we first write the integral as $$\int_0^M \sin(x^3) \,dx = \int_0^\infty \sin(x^3) \,dx - \int_M^\infty \sin(x^3) \,dx .$$

Using residue calculus or the Laplace transform gives that the first integral on the right, which gives the constant term of the series, has value $$\int_0^\infty \sin(x^3) \,dx = \frac16 \Gamma\left(\frac13\right) .$$ Applying integration by parts to the second integral on the right with $u = \frac1{x^2}$, $dv = x^2 \sin(x^3) \,dx$ gives $$- \int_M^\infty \sin(x^3) \,dx = - \frac1{3 M^2} \cos (M^3) + \frac23 \int_M^\infty \frac{\cos(x^3)}{x^3} \,dx ,$$ and again applying integration by parts to the integral on the right gives that it decays as $O\left(M^{-5}\right)$.

Answer 2

You want to compute the number $N$ of terms to be added such that $$\frac{\pi ^{2(3 N+5)}}{2\, (3 N+5)\, \Gamma (2 (N+2))}~\leq~ 10^{-k}$$ that is to say $$(3 N+5)\, \Gamma (2 (N+2))~\geq~\frac 12 \,\pi ^{2(3 N+5)}\,10^{k}$$ Taking logarithms and using Stirling approximation, the equation to be solved is $$0=2 N\log(N)-2N\log \left(\frac{e \pi ^3}{2}\right)+\frac 92\log(N)+\log \left(\frac{96 }{10^k\,\pi ^{19/2}}\right)+O\left(\frac{1}{N}\right)$$ Neglecting the isolated logarithm this would give, as an overestimate, $$N \sim \frac {e\pi^3}2\,W(t)\quad \text{where} \quad t=-\frac{1}{2 e \pi ^3}\log \left(\frac{9216 }{10^{2k}\,\pi ^{19}}\right)$$ $W(t)$ being Lambert function.

For $k=2$, the above gives $N=48$ while the exact value should be $40$.