60

I have a confession to make: none of the proofs of Sylow's theorems I saw clicked with me. My first abstract algebra courses were more on the algebraic side (without mention of group actions and geometric motivation for groups, except hastily mentioned dihedral groups), so when I (in self-study) discovered interplay between geometry and group theory, I was delighted. Many concepts and ideas suddenly made more sense to me.

I see Sylow's theorems as an useful technical black box, which can help you characterize groups when you only know numerical data about them. I've solved enough problems using those theorems, and now I'm interested if there is a way to make them ''click''.

I'm interested is there a geometrical idea behind Sylow's theorems (at least one of them), or at least a nice intuitive explanation of why that result should hold. How do you think about them?

ante.ceperic
  • 5,441
  • 5
    Wielandt's proof of the Sylow theorems is very transparent: you take all subsets (not subgroups) of order $p^n$ of $G$ [$p^n$ the biggest power of $p$ dividing $|G|$], and you let $G$ act via right multiplication. Counting mod $p$ shows that (at least) one of the orbits of these actions has order coprime to $p$. The stabilizer of such an orbit is a Sylow subgroup. Note that the key to making this work is using the largest power of $p$ that divides $|G|$: this is what allows you to find that "exceptional" orbit. –  Oct 09 '13 at 22:30
  • Looking at the action on the set of maximal $p$-subgroups (i.e., maximal elements in the set of $p$-subgroups) by conjugation leads also quickly to Sylow's theorems, but requires Cauchy's theorem as starting point. – j.p. Oct 10 '13 at 10:24
  • 3
    For connections between Sylow's theorems and geometry take also a look at this answer by Vipul Naik to a similar question or at the article Subgroup complexes by Peter Webb, pp. 349-365 in: ed. P. Fong, The Arcata Conference on Representations of Finite Groups, AMS Proceedings of Symposia in Pure Mathematics 47 (1987). – j.p. Oct 10 '13 at 10:28
  • user641 notice this proof: https://math.stackexchange.com/a/1593829/1216987 being largest is not crucial. – ZhenRanZR Nov 13 '24 at 06:28

3 Answers3

26

The theorems are stated purely algebraically or arithmetically (number of subgroups). Thus, I found it difficult to get geometirc intuition behind this one. However, I would say at least, that these theorems can be very nicely understood with some very concrete examples. The one I will illustrate is $S_4$.

The group $S_4$ has order $2^3.3$. Instead of thinking this group as permutation group, we can geometrically understand it in more interesting way: it is the group of rotational symmetries of cube. The cube has four diagonals, and the group of rotations of cube permutes these diagonals, which allows us to understand the group as $S_4$. What next?

enter image description here

Consider the rotational symmetries of cube through each diagonal: there will be three such rotations, forming a subgroup of order $3$; this is then a Sylow-$3$ subgroup. Thus, four diagonals will give four Sylow-$3$ subgroups (their cardinality is $\equiv 1(\pmod 3)$. What about conjugacy? If $\rho$ is a rotation taking diagonal $D_1$ to another diagonal $D_2$, then the rotation subgroup corresponding to $D_1$, which form Sylow-$3$ subgroup, is conjugate to the rotation subgroup corresponding to $D_2$, the conjugation is obtained by $\rho$. This proves conjugacy of Sylow-$3$ subgroups. Thus, the three Sylow theorems verified for prime $p=3$.

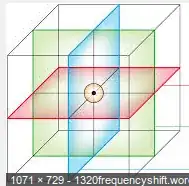
What about Sylow-$2$ subgroups? They also can be seen in interesting way: there are three planes which bisect cube, and are parallel or perpendicular to planes of cube. The rotations of cube which take, say blue plane to itself, form dihedral group of order $8$, and thus, three planes give three Sylow-$2$ subgroups, so they are in number $\equiv 1\pmod 2$. Since blue plane can be moved to green or red plane by some rotational symmetry of cube, this gives the conjugacy of Sylow-$2$ subgroups. enter image description here

p Groups
  • 10,458
12

I am not sure if that answer your question. There is a similar statement (The Cartan theorem) in compact Lie groups, which says that every maximal torus $T$ in a compact Lie group $G$ are conjugate to each other.

A maximal torus in a Lie group G is a connected maximal abelian subgroup. e.g. if $G = U(n)$ is the group of unitary matrices in $\mathbb C^n$, then $T$ is the set of diagonal matrices in $U(n)$.

Cartan theorem corresponds to Sylow theorem (every $p$-subgroup of a finite group $G$ are conjugate to each other). Recall that to prove Sylow theorem, one use the map $G/H \to G/H$ defined by left multiplication and argue that a fixed point exist (by counting). One can use exactly the same argument to prove Cartan theorem, but this time one uses Lefschetz fixed point formula to argue that the map $G/T \to G/T$ has a fixed point.

Such a proof can be found in Danial Bump's GTM book on Lie groups.

  • 3
    Except the Sylow subgroups aren't abelian. There's something to the analogy, but the Sylow theorem also asserts the existence, unless Cartan says something about the dimension of the maximal tori. – Thomas Andrews Oct 09 '13 at 23:21
  • 1
    Well there is the proof where you first embed your group in some $GL(n,p)$, and then prove the Sylow subgroup theorem there. The idea is somewhat geometrical, in that you look at the collection of upper triangular matrices. –  Oct 10 '13 at 02:16
  • 4
    @ThomasAndrews I don't know whether this is due to Cartan or to someone later, but, for a maximal Cartan $T$, the Euler characteristic of $G/T$ is always nonzero. This is analogous to the fact that $|G/P| \not \equiv 0 \bmod p$. – David E Speyer Dec 07 '14 at 16:58
  • 6
    Another analogy is maximal unipotent subgroups in complex linear algebraic groups. http://groupprops.subwiki.org/wiki/Maximal_unipotent_subgroup Again, any two maximal unipotents are conjugate, and maximal unipotents are always nilpotent (like $p$-groups are). And, unlike tori, unipotents don't have to be abelian. I don't know an easy way to talk about the dimension of the maximal unipotent though. – David E Speyer Dec 07 '14 at 17:01
6

I highly recommend going to a particular text: Visual Group Theory by Nathan Carter.

He brings group concepts to life by using (colored!) Cayley diagrams. Chapter 9 deals specifically with Sylow theory. He gives many geometric arguments.

On amazon: https://www.amazon.com/gp/aw/d/088385757X/ref=mp_s_a_1_sc_1?ie=UTF8&qid=1475779425&sr=8-1-spell&pi=AC_SX236_SY340_FMwebp_QL65&keywords=vosual+group+thwory

Zach Haney
  • 286