I need help in this proposition:
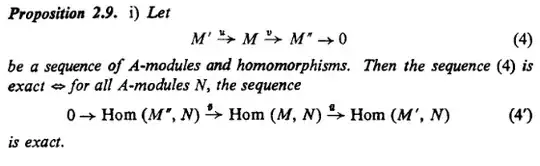

I'm sure it's a silly doubt, but I couldn't understand why $\overline v\ \text{injective}\ \forall N\implies v\ \text{surjective}$.
Thanks
I need help in this proposition:
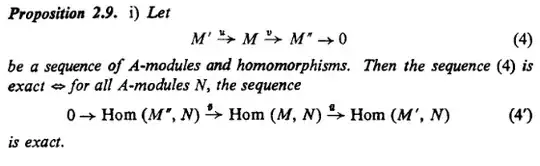

I'm sure it's a silly doubt, but I couldn't understand why $\overline v\ \text{injective}\ \forall N\implies v\ \text{surjective}$.
Thanks
Choose $N = M''/\operatorname{im}v$. If $v$ is not surjective, the canonical homomorphism $\varphi \colon M'' \to N$ is not zero. But $\overline{v}(\varphi) = \varphi \circ v = 0$.
$\DeclareMathOperator{\coker}{coker}\DeclareMathOperator{\hom}{hom}\DeclareMathOperator{\set}{Sets}$My hint in the previous revision must have been too short; I will write out what I was thinking. By the way, my deleted answer can simply be dualized by working, as I did below, in a more general category.
Proposition. Let $\mathcal C$ be a category, then an arrow $f:A\to B$ in $\mathcal C$ is an epimorphism if and only if the natural transformation $f^\ast:\hom(B,-)\to\hom(A,-)$ is a monomorphism in the category $\set^{C^{op}}$.
Proof. Note that $f^\ast$ is monic if and only if $\bar f=f^\ast_C:\hom(B,C)\to\hom(A,C)$ is monic for every object $C$ of $\mathcal C$. This is follows from the simple fact: let $\mu,\eta$ be natural transformations; $f^\ast\circ\mu=f^\ast\circ\eta$ iff for every $C$, $f^\ast_C\circ\mu_C=f^\ast_C\circ\eta_C$. Thus, we may fix our choice of $C$. We have, $\bar f$ is monic iff $\bar f$ is injective (it is an arrow in $\set$) iff $gf=hf$ for all $g,h\in\hom(B,C)$ implies $g=h$ iff $f$ is epi in $\mathcal C$. $\square$
Corollary. $f:M'\to M$ is a surjective $A$-module morphism if and only if $\bar f:\hom(M,N)\to\hom(M',N)$ is injective for every $A$-module $N$.
Proof. We just have to note that $f$ is surjective if and only if $f$ is epi in the category of $A$-modules. For the uninitiated, you use the equation $0\circ f=\coker f\circ f$. $\square$