It is possible to make equivalences among differential equations that share solutions?
I am thinking in two non-linear ODEs such they share the same solution of finite duration holding uniqueness among the initial time $t=0$ and until the finial extinction time $T=4$ which is a singular point, so, uniqueness on $t\in[0,\,4)$:
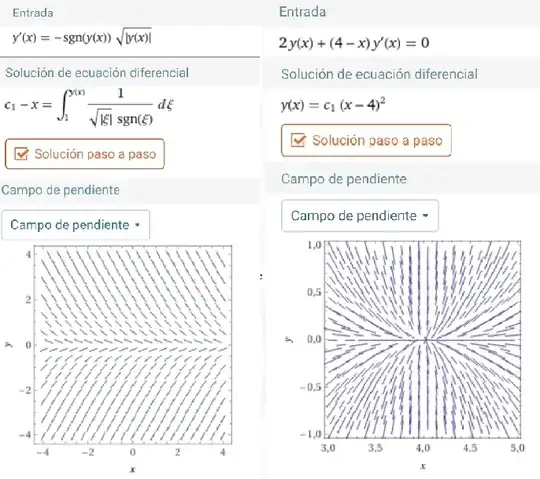
- $$y'=-\operatorname{sgn}(y)\sqrt{|y|},\quad y[0]=4 \quad \Rightarrow\quad y(t)=\frac{1}{4}(4-t)^2\theta(4-t) \tag{Eq. 1}\label{Eq. 1}$$
- $$2y+(4-t)y'=0,\quad y[0]=4 \quad \Rightarrow\quad y(t)=\frac{1}{4}(4-t)^2\theta(4-t)\tag{Eq. 2}\label{Eq. 2}$$
where $\theta(t)$ is the Heaviside step function. Here a plot in Demos showing the solution satisfies both differential equations with same initial condition.
Questions
It is possible to treat both equations as equivalent?, or at least, if It is possible to make some kind of equivalences among them? This because is easier to analyse (at least for me) the \eqref{Eq. 2} than \eqref{Eq. 1}, but I am interested in understand the behavior of \eqref{Eq. 1} through \eqref{Eq. 2}, as example... How could I have realize both equation share the same solution for some initial condition without knowing the solutions beforehand?
I am thinking in a general case by the way, no just this specific example.
Since the lack of answers I added later this comment:____________
As an example of what I am thinking/aiming to do: imagine I am working on a system modeled by something like \eqref{Eq. 1} but I don't know the answer yet, if I try to apply the Fourier Transform to find the solution $y(t)$ I would get stuck because of the nonlinear terms.
But if somehow I could demonstrate (I don't know how, maybe through Lyapunov's or Filippov's analysis), that the same solution of \eqref{Eq. 1} solves also \eqref{Eq. 2} (which I know it is possible because it actually happen in the example), I could try then to find the solution $y(t)$ by means of applying the Fourier Transform to \eqref{Eq. 2} (which maybe in this case make little sense, but it is an example - I reviewed it now at the 3nd added later).
Also, if somehow I am able to find the time $T$ when it stops moving and its final position $y[T]$, maybe I could made some approximation by using what I asked in this question and find the solution by Fourier or Laplace's means, es example, If I look for a system that decays oscillating (like this one as example), I could try to match it with the following frustrated 2nd order ODE and take the Fourier Transform between times $t=0$ and $t=T$:
$$h(t)=y(T)-(y(T)-y(t))\theta(T-t) \Rightarrow h''+ah'+bh+c-(bh(T)+c)\theta(t-T)=0 $$
And find the original equation's solution by the Fourier transform of this replacement equation: Does this makes any sense?
*2nd added later - answer to @DWade64 comment
Their fields look very different indeed in Wolfram-Alpha, only similar on the neighborhood of the solution.
3nd added later - not mandatory reading
Here I just were trying my hypothesis for \eqref{Eq. 2}:
$$\begin{array}{c} 2y[t]+(4-t)y'[t]=0\qquad \Biggr/\mathbb{F}\{\cdot\}\\ \Rightarrow 2\hat{y}-4iw\hat{y}-i\frac{\partial}{\partial w}\left(iw\hat{y}\right) = 0\\ \Rightarrow 2\hat{y}-4iw\hat{y} -i\left[i\hat{y}+iw\hat{y}'\right] = 0\\ \Rightarrow \left(3-4iw\right)\hat{y}+w\hat{y}'=0 \end{array}$$ Here I got an ODE for the Fourier Transform $\hat{y}$ which Wolfram-Alpha solves as: $$\hat{y}(iw) = c_1\frac{e^{4iw}}{w^3}$$ and taking the inverse Fourier Transform on Wolfram-Alpha (here I match constants since I am used to work with the electrician definition) I get: $$y(x)=c_1\frac{i}{4}(t-4)|t-4|$$ and matching the initial value $y[0]=4$ I find $c_1=i$ so I recover for $0<t<4$: $$y(x)=\frac{1}{4}(4-t)|4-t|,\quad \hat{y}(iw) = i\frac{e^{4iw}}{w^3}$$
So, at least in principle, If it is possible to find somehow that the solution of \eqref{Eq. 1} matches the solution of \eqref{Eq. 2}, it could have been possible to find the solution of \eqref{Eq. 1} by solving \eqref{Eq. 2} knowing beforehand it will hold only between $t\in\{0,\,T=4\}$.
Keep in sight that it is not exactly the same solution so it is not also exactly the same spectrum 1 spectrum 2:
$$\int\limits_{-\infty}^{\infty} \frac{1}{4}(4-t)^2\theta(4-t)e^{-iwt}\,dt = 4\pi\delta(w)- i\frac{e^{4iw}}{2w^3}$$
$$\int\limits_{0}^{\infty} \frac{1}{4}(4-t)^2\theta(4-t)e^{-iwt}\,dt = \frac{i+w(4-8iw)}{2w^3}-i\frac{e^{4iw}}{2w^3}\equiv \int\limits_{0}^{4} \frac{1}{4}(4-t)^2\theta(4-t)e^{-iwt}\,dt$$
when you could notice the the upper bound of the integral don't change the result since the solutions do have stopped moving at time $t=4$.
4th Added later
Just as curiosity, the same solution of \eqref{Eq. 1} and \eqref{Eq. 2} solves for $0\leq t<4$: $$y''=-\frac{1}{2}\operatorname{sgn}(y'),\quad y[0]=4,\,y'[0]=-2 \quad \Rightarrow\quad y(t)=\frac{1}{4}(4-t)^2\theta(4-t) \tag{Eq. 3}\label{Eq. 3}$$
Here added in Desmos.