Which small groups appear in multiple classical families like $C_n$, $D_n$, $S_n$, or $A_n$?

Question

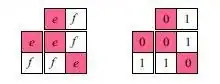
On page 90 of Visual Group Theory by Nathan Carter, there's an exercise (Exercise 5.20) that points out an interesting phenomenon: some small groups belong to more than one of the classical group families — cyclic $C_n$, dihedral $D_n$, symmetric $S_n$, and alternating $A_n$ — when considered up to isomorphism.

For example, the book notes that $D_1$, a degenerate dihedral group with two elements, has the same group structure as the cyclic group $C_2$. Their multiplication tables match, modulo the names of the elements.

My Question

What other small groups (say, with order $\leq 12$) are shared across these families in the sense that they are isomorphic? Are there, for example, any groups in the $D_n$ family that are isomorphic to a group in $S_n$, $A_n$, or $C_n$?

I'm trying to build intuition for recognizing structural similarities between groups that arise in different contexts, and I’m curious about how frequently this overlap occurs among these well-known families.

Answer 1

(As you did in your question, I will be using $D_n$ to refer to the dihedral group on $n$ letters, not the dihedral of order $n$.)

Many small groups in these families are isomorphic to the trivial group:

$$\{e\} \cong C_1 \cong D_0 \cong S_0 \cong S_1 \cong A_0 \cong A_1 \cong A_2$$

As you pointed out, $C_2 \cong D_1$, and both of these groups are isomorphic to $S_2$ (they all have one nontrivial element, which is a transposition):

$$C_2 \cong D_1 \cong S_2.$$

We also have

$$S_3 \cong D_3,$$

which represents the fact that the rigid symmetries of a triangle make up all the permutations of its vertices, and

$$C_3 \cong A_3,$$

which represents that fact that the rotations of a triangle make up the even permutations of its point (since all reflections are themselves single transpositions, and each rotation can be decomposed as two transpositions).

Once we go over groups of order $6$, there are no more isomorphisms between these families as the rotations and reflections of $n$ points do not cover all the permuations (nor all the even permutations) of the points. However, for more isomorphisms between small finite groups, see this Wikipedia page. Also see this list of small groups up to isomorphism (also Wikipedia).

Answer 2

You can consider all the possibilities, and exhaust them rather easily. (I just use $=$ and $\neq$ instead of $\simeq$ and $\not\simeq$.)

• $C_n=D_m$? This is possible only if $D_m$ is abelian, which happens when $m=1$. In that case, $n=2$, and $C_2=D_1$ which you mention as well.
• $C_n=S_m$? Same as above, we get $m=1$ or $m=2$. This gives $C_1=S_1$ and $C_2=S_2$.
• $C_n=A_m$? Same as above, we get $m=2$ or $m=3$. This gives $C_1=A_2$ and $C_3=A_3$.
• $D_n=S_m$? The centre of $D_n$ has size exactly half of it. The only subgroup of $S_m$ of half its size is $A_m$. Thus, $C_n=A_m$, which gives $(n,m)=(1,2)$ or $(n,m)=(3,3)$. Indeed, $D_1=S_2$ and $D_3=S_3$.
• $D_n=A_m$? If $n=1$, we don't get anything. If $n>1$, then $D_n$ is not simple. But $A_m$ is simple for $m=3$ and $m\ge5$. The only possibilities are $m=2$ and $m=4$. For $m=2$, we get $2n=1$, absurd. For $m=4$, we get $n=12$. But $D_{12}\neq A_4$. (No element has order $12$ in $A_4$.)
• $S_n=A_m$? That gives $2\cdot n!=m!$. If $n>1$, we get $n!<2\cdot n!<(n+1)n!=(n+1)!$, which cannot be. So, $n=1$. Then, $S_1=A_2$.

Thus, we can list all of this together:

• $C_1=S_1=A_2$.
• $C_2=D_1=S_2$.
• $C_3=A_3$.
• $D_3=S_3$.

Hope this helps. :>