Prove $\int_0^\theta\log\left(\cos x-\sqrt{\cos^2x-\cos^2\theta} \right)dx=(\theta+\frac{\pi}{2})\log(\cos\theta)$ for $0<\theta<\frac{\pi}{2}$

Question

Let $I(\theta)=\int_0^\theta\log\left(\cos x-\sqrt{\cos^2x-\cos^2\theta}\right)dx$ for $0<\theta<\frac{\pi}{2}$.

Prove that $I(\theta)=\left(\theta+\frac{\pi}{2}\right)\log(\cos\theta)$.

Context

The question arose when I was investigating the following geometry question.

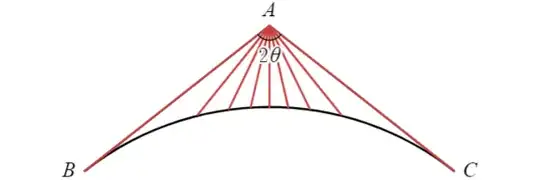
Tangents to a circle at $B$ and $C$ meet at $A$. Let $\angle BAC=2\theta$. Draw $n$ line segments from $A$ to minor arc $\overset{\huge\frown}{\rm{BC}}$, equally spaced in terms of angles, with two of the line segments coincident with the tangent lines. Here is an example with $n=9$.

If $\lim\limits_{n\to\infty}(\text{product of lengths of the line segments})$ is a positive real number, then what is $AB$ in terms of $\theta$ ?

Long story short: numerical investigation suggested that $AB=\left(\cos\theta\right)^{-\pi/(2\theta)}$ (which surprisingly does not contain $e$), which is true if and only if $I(\theta)=\left(\theta+\frac{\pi}{2}\right)\log(\cos\theta)$. (And this would imply that the limit of the product equals $AB$.)

The case $\theta=\frac{\pi}{4}$

$I\left(\frac{\pi}{4}\right)=\int_0^{\pi/4}\log\left(\cos x-\sqrt{\cos^2x-\frac12}\right)dx$, via $x\to\frac{x}{2}$, is equal to $-\frac34\int_0^{\pi/2}\log{(\sqrt{\cos x}+\sqrt{\cos x+1})}dx$, which is evaluated here. I don't know how to adapt this solution to the general case.

Answer 1

\begin{align} I(\theta)& =\int_0^\theta\ln\left(\cos x-\sqrt{\cos^2x-\cos^2\theta}\right)dx\\ & =\int_0^\theta\ln\frac{\cos^2\theta}{\cos x+\sqrt{\cos^2x-\cos^2\theta}}{} dx\\ &= \int_0^\theta \ln\cos\theta \ dx-\int_0^\theta \cosh^{-1}\frac{\cos x}{\cos\theta}\ dx\\ &= \theta \ln\cos\theta -\int_0^\theta d_y\bigg( \int_0^y \cosh^{-1}\frac{\cos x}{\cos y} dx\bigg)\\ &= \theta \ln\cos\theta- \int_0^\theta \int_0^y \frac{\tan y \cos x}{\sqrt{\cos^2x-\cos^2y}} dx\ dy\\ &= \theta \ln\cos\theta- \int_0^\theta \frac\pi2\tan y\ dy=\left(\theta+\frac\pi2\right) \ln\cos\theta \end{align}

Answer 2

Let : $$I(\theta) = \int^{\theta}_0 \ln(\cos(x)-\sqrt{\cos^2(x)-\cos^2(\theta)})dx$$ Using Leibniz integral rule therfore: $$I'(\theta)=\ln(\cos(\theta)) -\int^{\theta}_0 \frac{\sin(\theta)\cos(\theta)}{\sqrt{\cos^2(x)-\cos^2(\theta)}(\cos(x)-\sqrt{\cos^2(x)-\cos^2(\theta)})}dx$$

we have using wolfram alpha : \begin{align*} I&=\int \frac{1}{\sqrt{\cos^2(x)-\cos^2(\theta)}(\cos(x)-\sqrt{\cos^2(x)-\cos^2(\theta)})} dx\\ &=\frac{x}{\cos^2(\theta)}+\frac{1}{\cos^2(\theta)}\arctan\left({\frac{\sin(x)}{\sqrt{\sin^2(x)-\sin^2(\theta)}}}\right)\end{align*}

Thus :

$$\int^{\theta}_0 \frac{1}{\sqrt{\cos^2(x)-\cos^2(\theta)}(\cos(x)-\sqrt{\cos^2(x)-\cos^2(\theta)})} dx=\frac{\theta}{\cos^2(\theta)}+\frac{\pi}{2\cos^2(\theta)}$$

therfore:

$$I'(\theta)=\ln(\cos(\theta)) -\frac{\theta\sin(\theta)}{\cos(\theta)}-\frac{\pi\sin(\theta)}{2\cos(\theta)}$$

finnally :

$$I(\theta)=C + \left({\frac{\pi}{2}+\theta}\right)\ln(\cos(\theta))$$

we have : $$I\left({\frac{\pi}{4}}\right)=-\frac{3\pi}{8}\ln(2) = C -\frac{3\pi}{8}\ln(2)$$ this implies that :$C=0$

Answer 3

First, we use the identity $$ \left(\cos x - \sqrt{\cos^2x-\cos^2\theta}\right)\left(\cos x + \sqrt{\cos^2x-\cos^2\theta}\right) = \cos^2\theta $$ Taking the logarithm of both sides gives $$ \log\left(\cos x-\sqrt{\cos^2x-\cos^2\theta}\right) = 2\log(\cos\theta) - \log\left(\cos x+\sqrt{\cos^2x-\cos^2\theta}\right) $$ Substituting this into the integral for $I(\theta)$ splits it into two parts: $$ I(\theta) = \int_0^\theta 2\log(\cos\theta) dx - \int_0^\theta \log\left(\cos x+\sqrt{\cos^2x-\cos^2\theta}\right)dx $$ $$ I(\theta) = 2\theta\log(\cos\theta) - J(\theta) $$ where $J(\theta) = \int_0^\theta \log\left(\cos x+\sqrt{\cos^2x-\cos^2\theta}\right)dx$. Now we need to show that $J(\theta) = \left(\theta - \frac{\pi}{2}\right)\log(\cos\theta)$ to complete the proof. We differentiate $J(\theta)$ with respect to $\theta$: $$ J'(\theta) = \log(\cos\theta) + \int_0^\theta \frac{\partial}{\partial\theta}\log\left(\cos x+\sqrt{\cos^2x-\cos^2\theta}\right)dx $$ The partial derivative of the integrand is $$ \frac{1}{\cos x+\sqrt{\cos^2x-\cos^2\theta}} \cdot \frac{\sin\theta\cos\theta}{\sqrt{\cos^2x-\cos^2\theta}} $$ By rationalizing the denominator, this simplifies to $\tan\theta\left(\frac{\cos x}{\sqrt{\cos^2x-\cos^2\theta}} - 1\right)$. Thus, $$ J'(\theta) = \log(\cos\theta) + \tan\theta \int_0^\theta \left(\frac{\cos x}{\sqrt{\cos^2x-\cos^2\theta}} - 1\right)dx $$ The integral term evaluates to: $$ \int_0^\theta \frac{\cos x}{\sqrt{\cos^2x-\cos^2\theta}}dx - \int_0^\theta 1\,dx $$ With the substitution $\sin x = u \sin\theta$, the first integral becomes $\int_0^1 \frac{du}{\sqrt{1-u^2}} = \frac{\pi}{2}$. The second is simply $\theta$. So the integral term is $\frac{\pi}{2}-\theta$. Substituting this back, we get the derivative of $J(\theta)$: $$ J'(\theta) = \log(\cos\theta) + \tan\theta\left(\frac{\pi}{2}-\theta\right) $$ Which is the derivative of $\left(\theta - \frac{\pi}{2}\right)\log(\cos\theta)$: $$ \frac{d}{d\theta}\left[\left(\theta-\frac{\pi}{2}\right)\log(\cos\theta)\right] = \log(\cos\theta) + \left(\theta-\frac{\pi}{2}\right)\left(\frac{-\sin\theta}{\cos\theta}\right) = \log(\cos\theta) + \left(\frac{\pi}{2}-\theta\right)\tan\theta $$ Since the derivatives are equal, $J(\theta)$ must be of the form $\left(\theta - \frac{\pi}{2}\right)\log(\cos\theta) + C$. $C$ is zero by considering the limit as $\theta \to 0^+$, since $J(0)=0$. Therefore $$ J(\theta) = \left(\theta - \frac{\pi}{2}\right)\log(\cos\theta) $$ Substituting this back into the expression for $I(\theta)$: $$ I(\theta) = 2\theta\log(\cos\theta) - \left(\theta - \frac{\pi}{2}\right)\log(\cos\theta) = \left(\theta + \frac{\pi}{2}\right)\log(\cos\theta) $$

Therefore, $$\boxed{I(\theta) = \left(\theta + \frac{\pi}{2}\right)\log(\cos\theta)}$$