2

I wanted to find $\cos 7.5^\circ$, so I did what anyone would do; I used the cosine half angle formula. Hence we get $$\cos 7.5^\circ = \sqrt{\frac{1+\cos 15^\circ}{2}} = \sqrt{\frac{1}{2} + \frac{1}{4}\sqrt{\frac{3}{2}} + \frac{1}{8}\sqrt2}$$ which is, well, horrible. Therefore, I want to denest this ugly thing. So, I assumed the whole thing to be equal to $\sqrt{p} + \sqrt{q} + \sqrt{r}$, but after squaring both sides I did not know what to assume to be equal to what. We can also use the half angle formula that uses $\sin x$. $$\cos 7.5^\circ = \frac{\sqrt{4 + \sqrt6 - \sqrt2} + \sqrt{4 - \sqrt6 + \sqrt2}}{4}$$ This too needs some denesting. How do we do it? Also, if someone can find a nice geometrical way or virtually anything else, just denested and looking all nice, I will accept it. Here's a similar question.

Blue
  • 83,939
Supernerd411
  • 689
  • 4
    Note that $\sqrt{3/2} = \sqrt{6}/2$, so we can rewrite this as $\sqrt{1/2 + 1/8 \cdot \sqrt{6} + 1/8 \cdot \sqrt{2}} = \sqrt{(4 + \sqrt{6} + \sqrt{2})/8} = 1/2 \cdot \sqrt{4 + \sqrt{2} + \sqrt{6}}$, which may be easier to solve. – Johannes Kloos Jun 13 '25 at 12:59
  • @JohannesKloos Yes, but they obey the same general pattern – Supernerd411 Jun 13 '25 at 13:07
  • It doesn't look promising. I gave this to sympy and it returned $\frac{\sqrt{\frac{1}{2} - \frac{\sqrt{2}}{4}}}{2} + \frac{\sqrt{3} \sqrt{\frac{\sqrt{2}}{4} + \frac{1}{2}}}{2}$ – Duong Ngo Jun 13 '25 at 13:15
  • To expand on Johannes's comment, under the root you have an element of $\mathbb Q[\sqrt 2,\sqrt 3]$, so you'd want to solve $(a+b\sqrt 2 + c\sqrt 3 + d\sqrt 6)^2 = e(4+\sqrt 2 + \sqrt 6)$ over integers, but that doesn't seem to have non-trivial solutions. – Ennar Jun 13 '25 at 13:31
  • @Ennar You've got two negatives there... Does it seem to have trivial solutions then? – Supernerd411 Jun 13 '25 at 13:49
  • Yes, it seems to have trivial solution $a=b=c=e=d=0$, but that's not what I said. I said that there are no other solutions. In other words, you can't denest further. – Ennar Jun 13 '25 at 13:53
  • Do you mind giving a mathematically sound definition of „horrible“? – wasn't me Jun 13 '25 at 14:13
  • 1
    @wasn'tme, apparently, being an element of algebraic extension of degree $8$. – Ennar Jun 13 '25 at 14:16
  • @wasn'tme Yes, er, whatever Ennar said. – Supernerd411 Jun 13 '25 at 14:26
  • You cannot de-nest radicals the way you can eg expand brackets raised to positive integer powers - it just doesn’t work like that. You might be trying something impossible. – SBK Jun 13 '25 at 15:35

1 Answers1

1

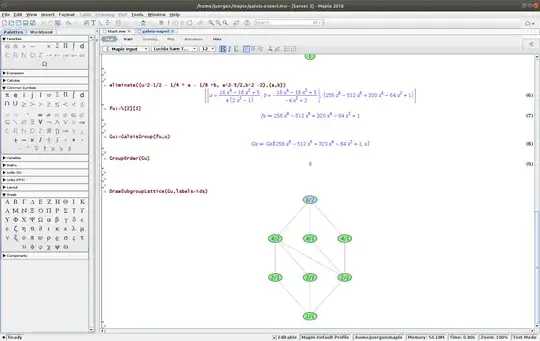
If it is your goal to write the nested radical expression that I call $u$ here as a rational combination of square roots of rational numbers you can see that this is not possible from the following calculation with Maple where I calculated the subgroup lattice of the galois group of the minimal polynomial of $u$:

enter image description here

You see that the three subgroups of order $4$ do not intersect in the trivial subgroup, but in the group labeled $2/1$ in the diagram below.

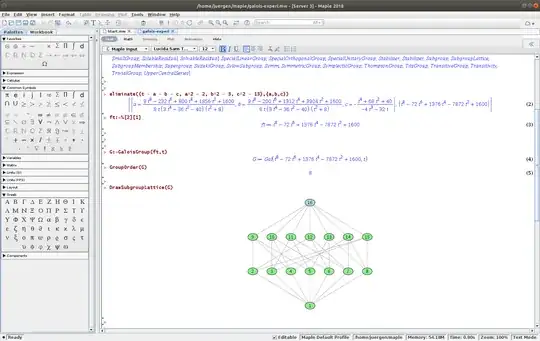
On the contrary the following shows a similar calculation for $t = \sqrt{2}+\sqrt{3}+\sqrt{13}$ where the subgroup lattice looks obviously totally different.

enter image description here

Jürgen Böhm
  • 3,280