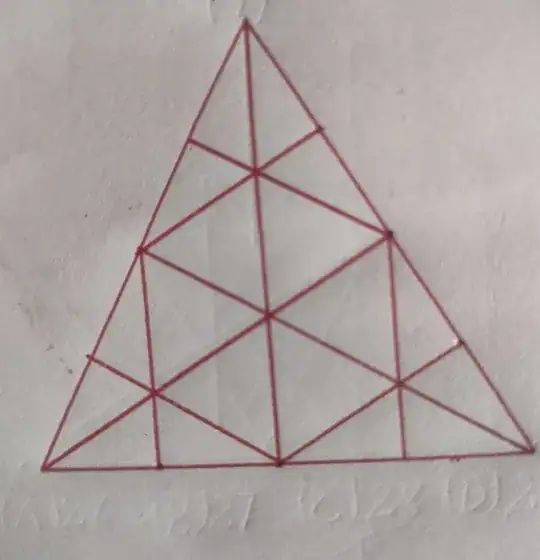
How many triangles are there.

Question

In this figure, there are 12 straight lines. With the help of 12 lines, 220 triangles can be construct by 12C3 rule of combination. There are 7 points from which 3 straight lines meets so 7 triangles are eliminated. There are 3 such points from which 4 lines passes through a common point so 3×4C3=12 triangles eliminated. There are 3 set of parallel triplets lines so 10×3C1×3=90 triangles are eliminated. So total triangles that actually formed = 220-7-12-90+1(outermost triangle)=112. Am I right? Correct me if I'm wrong.

You would be right if the question was dealing with lines, not line segments. Notice how some of the triangles you've included in your count can only be formed when you extend some segments beyond the big triangle. — Amogh, May 23 '25 at 04:02
This is your sixth question asking how many triangles there are in some figure or another. What is the point? — Gerry Myerson, May 23 '25 at 04:45
@Gerry Myerson, You are right sir. The point is that I wants to learn something more and new concepts. — Mathematical science, May 23 '25 at 05:10
OK. Have you learned anything from the fifth question than you couldn't have learned from the first four? — Gerry Myerson, May 23 '25 at 05:24

score 2 · Answer 1 · answered May 23 '25 at 14:10

Too long for a comment.

I have counted 46 triangles. The method of the counting is the following. I split the lines in 4 classes: 3 external boundaries and 3 classes of parallel lines each containing 3 lines. Then I considered the following classes of triangles according to the number of sides lying on the external boundary: 0) no, 1) one, 2) two, 3) three.

The triangles of class 0 are contained in the central hexagon and there are $6$ of them.

The triangles of the class 1 can be counted as follows. Choose a boundary side. The set of the other two sides of a triangle either contains a perpendicular line to the boundary or not. There are four triangles if it contains the perpendicular line and three triangles in the other case. Altogether we have $3\cdot(3+4+4)=33$ such triangles.

The triangles of the class 2 consist of two boundary side and a side perpendicular to one of them. For each pair of boundary side we have 4 such triangles which sum up to $3\cdot4:2=6$.

There is a single triangle of the class 3.

Altogether we have $6+33+6+1=46$ triangles.

Yes: $12$ of one smallest triangle, $6+6$ of two smallest triangles or a small equilateral triangle, $6$ of three smallest triangles, $6$ of two smallest triangles and a small equilateral triangle, $3$ of a third of the biggest triangle, $6$ of half of the biggest triangle, and $1$ of the whole biggest triangle. So $46$ in total. Similar question to https://math.stackexchange.com/questions/5069085 — Henry, May 23 '25 at 15:20

How many triangles are there.

1 Answers1