1

The proof is in the images below: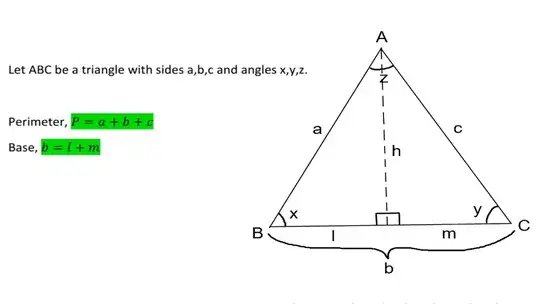1

2

3

4 5

Is this proof valid ? Could this be used to derive further equations ?

T-Rex_Prime
  • 29
  • 5
  • 2
    See also: https://math.stackexchange.com/questions/2367978/between-all-the-triangles-with-p-1-find-the-ones-with-a-max?noredirect=1 I found it through Approach zero search engine. – User May 20 '25 at 20:01
  • 1
    @User Cool! Totally different approach to same formula. – T-Rex_Prime May 20 '25 at 20:14

1 Answers1

0

Yes, the final formula you derived (enclosed in the red border) is correct. Here is another result that can be obtained from this result.

The law of sines can be used to derive the following well-known result for the area $A$ of any triangle : \begin{equation} A=\tfrac{1}{2}ac\sin z=\tfrac{1}{2}ab \sin x =\tfrac{1}{2}bc \sin y \tag{1} \end{equation} By equating any of the expressions for the area in (1) with the area formula presented here, one can simplify to obtain each of the following identities that relate sides to angles : \begin{equation} ab=\frac{p^2\sin y\sin z}{(\sin x+\sin y + \sin z)^2}\ ,\ bc=\frac{p^2\sin x \sin z}{(\sin x + \sin y +\sin z)^2}\ ,\ ac=\frac{p^2\sin x \sin y}{(\sin x +\sin y +\sin z)^2}, \end{equation}

from which one can obtain the following equalities which resemble the law of sines :

\begin{equation} \frac{(\sin x+\sin y+\sin z)^2}{p^2}=\frac{\sin y\sin z}{ab}=\frac{\sin x\sin z}{cb}=\frac{\sin x\sin y}{ca}. \end{equation}

Timothy
  • 322