4

I am looking for an (if possible constructive) classification of those finite, simple graphs (no loops, no multi-edges), where the open neighbourhood of each vertex (excluding that vertex aka open neighbourhood) is isomorphic to $C_7$; equivalently, where the closed neighbourhood of each vertex including that 'central' vertex is isomorphic to the wheel graph $W_8$ with 7 spokes

W8 graph

Alternatively, theses graphs are called 'locally $C_7$ (open)'.

Is there a classification of the finite, simple graphs that are locally $C_7$ (open neighbourhood definition)?

I understand that there is some relationship to triangulations or 'polyhedral realizations' of Hurwitz surfaces (https://en.wikipedia.org/wiki/Hurwitz_surface) that exist only for certain values of the genus (https://oeis.org/A179982); which would suggest a respective infinite set of locally $C_7$ graphs.

References

Examples

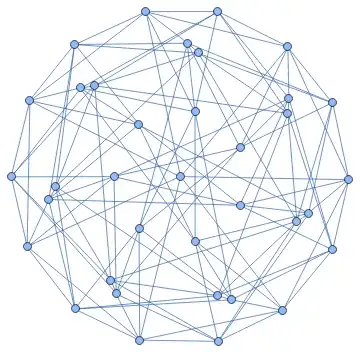
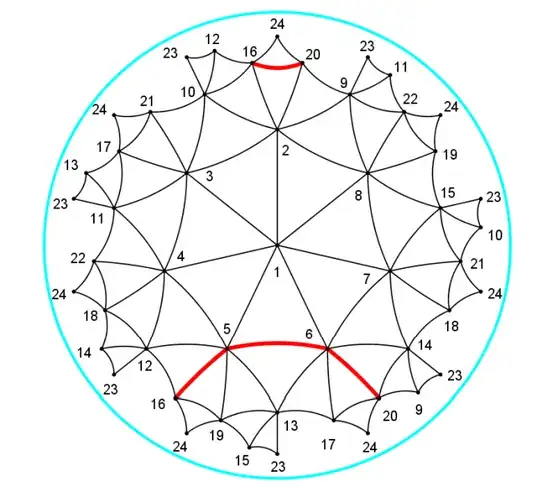
  1. The 7-regular Klein graph has 24 vertices and 84 edges - also see https://houseofgraphs.org/graphs/1198. The graph automorphism group has order 336 and can be embedded in the genus-3 orientable surface. One of the 'best ways looking' at the graph is embedded in an order-7 triangular tiling identifying certain vertices on the border of the disk Klein graph
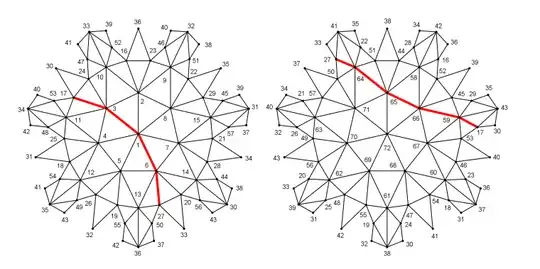
  2. The self-intersection-free, polyhedral realization of the Hurwitz surface of genus 7 aka Macbeath surface or Fricke-Macbeath surface with 72 vertices, 252, edges, 168 triangles and automorphism group of order 1008 (including orientation-reversing automorphisms) - see https://houseofgraphs.org/graphs/52273 Fricke-Macbeath graph

Additional example

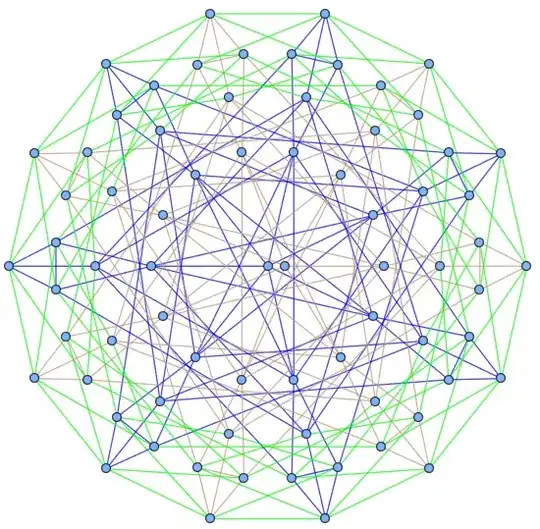
  1. The paper in the reference provides a $C_7$ graph with 36 vertices, 126 edges, 84 triangles and graph automorphism group of order 7. The genus is unknown.

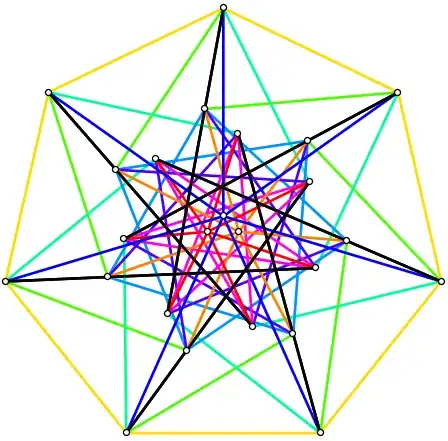
Here the 'high dimensional embedding'

Graph[ImportString[">>graph6<<cvjCSLgUI@G`GG?Ie?@?DCC?O?gO_??_SI?A@OP?GGO?_Cb?BCO?AO_?@@HW?EH_?_c???AA`WA@aC?E@?GS?CKgO?OOsO_CG`CP???@lg\n", "Graph6"], GraphLayout->"HighDimensionalEmbedding"]

C7 graph w 36 vertices

This example suggests that there are many more locally $C_7$ graphs - just not maximizing the automorphism group order for a given genus (the ones maximizing are the Hurwitz surfaces - examples 1 and 2 above).

References

Michael T
  • 1,742
  • 2
    Do you mean that for each $v\in V(G)$, the subgraph induced by $N(v)$ is $C_7$? Not just that $N(v)$ contains a $C_7$, I presume. – Shou May 22 '25 at 00:47
  • 2
    Hi Shou, yes, the subgraph induced by $N(v)$; not 'more' than $C_7$ in the open neighbourhood of each vertex $v$. – Michael T May 22 '25 at 09:29
  • Observe that the fact there's only countably many graphs like that is trivial, as there are only countably many (simple finite) graphs – Bruno Andrades May 23 '25 at 14:05
  • 1
    I don't really have a pen and paper right now to check if it's completely correct, but it seems like there is a bijection between the set of the isomorphism classes of connected finite simple graphs that are locally $C_7$ and the set of all conjugacy classes of torsion-free, finite-index subgroups of the $(2,3,7)$-triangle group. – HackR May 23 '25 at 15:08
  • Hi HackR, would that work for example 3 in the 'not an answer' answers below? Put differently, would that only cover high symmetry cases? BR – Michael T May 24 '25 at 08:02
  • Hi Bruno, I guess I meant the infinite set along the OEIS sequence... corrected. – Michael T May 24 '25 at 15:30
  • 1
    @MichaelT Ah! That's a nice catch. I think we need to drop the torsion-free condition. Your example 3 in fact comes from a torsion subgroup. – HackR May 25 '25 at 08:09
  • @HackR, thank you! BTW: Would you have a nice (short and accessible) reference to for the map from graphs ('mod automorphisms') to subgroups of the $(2,3,7)$-triangle group (mod conjugacy) or could you even explain it for the examples? BTW2: Would that help construct, say, the 10 $C_7$ graphs with fewest number of vertices? – Michael T May 25 '25 at 08:44

3 Answers3

0

Not an answer, but I posted an embedding of the Fricke-Macbeath graph.

enter image description here

Ed Pegg
  • 21,868
0

Not an answer either, 'just' another case (example 3, if you wish).
The paper in the reference provides a $C_7$ graph with 36 vertices, 126 edges, 84 triangles and graph automorphism group of order 7. The genus is unknown.

Here the 'high dimensional embedding'

Graph[ImportString[">>graph6<<cvjCSLgUI@G`GG?Ie?@?DCC?O?gO_??_SI?A@OP?GGO?_Cb?BCO?AO_?@@HW?EH_?_c???AA`WA@aC?E@?GS?CKgO?OOsO_CG`CP???@lg\n", "Graph6"], GraphLayout->"HighDimensionalEmbedding"]

C7 graph w 36 vertices

This example suggests that there are many more locally $C_7$ graphs - just not maximizing the automorphism group order for a given genus (the ones maximizing are the Hurwitz surfaces - examples 1 and 2 above).

Back to the classification and the need to find some approach for a construction...

References

Michael T
  • 1,742
0

Also not an answer. Connecting a set of extraordinary lines in the Braced Heptagon and adding three new points to the main 7-cycles gives a new embedding of the Klein graph.

Braced Klein Graph

Ed Pegg
  • 21,868