3

The book reference is here.

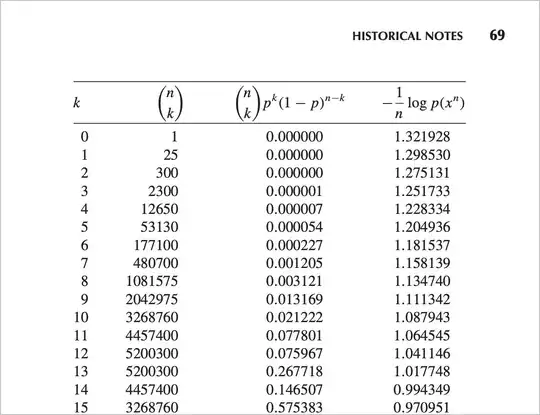
The problem $(3.13)$ concerns the typical set for a sequence of i.i.d. binary random variables, $X_{1}, X_{2},...,X_{25}$, where the probability that $X_i = 1$ is $0.6$ (and therefore the probability that $X_i = 0$ is $0.4$). This is essentially a sequence of flips of a biased coin. The entropy of a random variable with this probability is $.971$. The typical set comes up in the discussion of the $\mathrm{AEP}$ (asymptotic equipartition property).

Specifically, I think the third column in the book's table is wrong. I don't know if I am allowed to paste an image of that table here, so I am only going to post part of it.

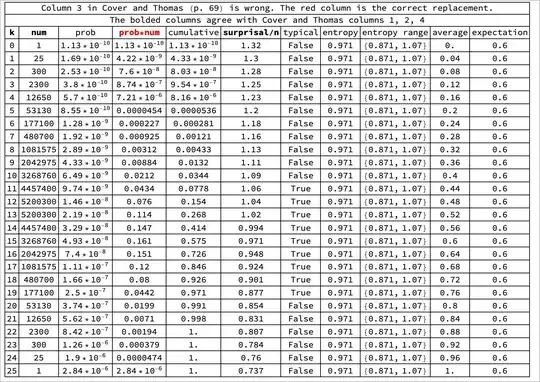
enter image description here

The table in the book has four columns. I think columns $1$, $2$, and $4$ are correct. I think column $3$ is wrong and should be replaced by the column prob$*$num in the table I independently generated.

In my table, I've added other columns related to the $\mathrm{AEP}$.

The formula for surprisal/n column is $-\log_2({\text{prob}})/n$ and is correct in both the book's table and mine. ($n = 25$).

Question: Do others agree? And, what IS the third column in the book?

enter image description here

Matthew Towers
  • 11,540
PaulCommentary
  • 131

2 Answers2

6

If $n=25$ and $p=0.6$ then the values in the first three columns for $k$ and ${n \choose k}$ and ${n \choose k}p^k(1-p)^{n-k}$ should be as follows.

Some of the third column in the book look correct on this basis but, as you say, some (particularly for odd $k$) are obviously wrong. It was probably a programming error or a copy and paste error.

    0       1 0.000000
    1      25 0.000000
    2     300 0.000000
    3    2300 0.000001
    4   12650 0.000007
    5   53130 0.000045 
    6  177100 0.000227
    7  480700 0.000925  
    8 1081575 0.003121 
    9 2042975 0.008843 
   10 3268760 0.021222
   11 4457400 0.043410 
   12 5200300 0.075967
   13 5200300 0.113950 
   14 4457400 0.146507
   15 3268760 0.161158
   16 2042975 0.151086
   17 1081575 0.119980
   18  480700 0.079986
   19  177100 0.044203
   20   53130 0.019891
   21   12650 0.007104
   22    2300 0.001937
   23     300 0.000379
   24      25 0.000047
   25       1 0.000003
Henry
  • 169,616
5

It appears that when $k$ is even, the numbers in third column of the book's table are the binomial probabilities $$\binom{25}{k} 0.6^k 0.4^{25-k}$$ just as advertised. However, for odd $k$, they are instead the cumulative binomial probabilities (also fully correct when rounded to the decimal places given) $$\sum_{i=0}^k \binom{25}{i} 0.6^i 0.4^{25-i}.$$ We can only speculate how this could have happened, but numerically speaking that's all there is to these numbers.

Misha Lavrov
  • 159,700