Prove concyclic points in a parallelogram

Question

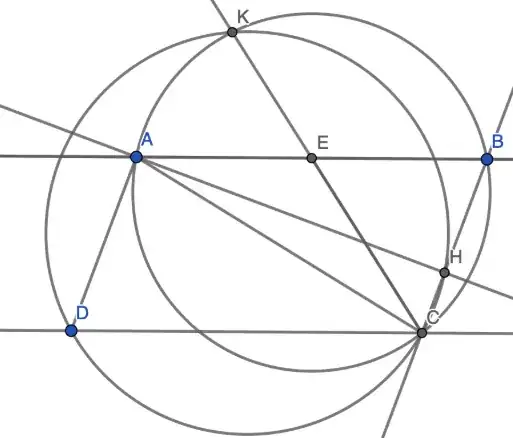
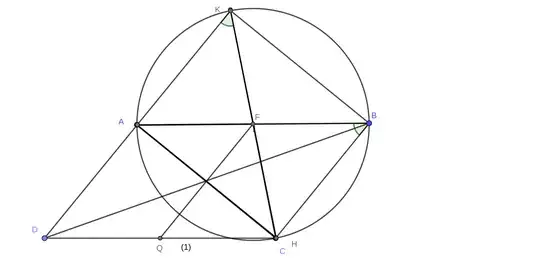
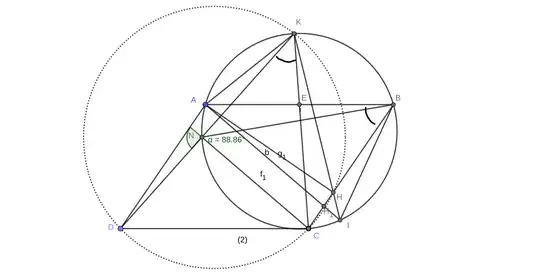
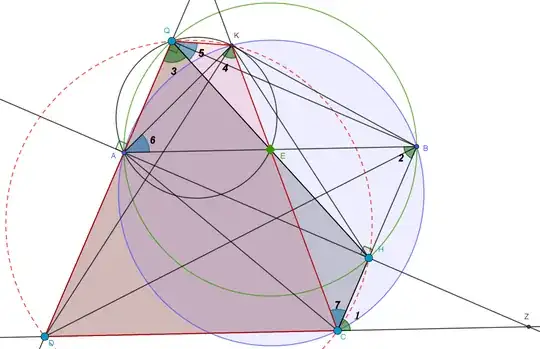
Let $ABCD$ be a parallelogram with obtuse angles at $A$ and $C$. Let $H$ be the foot of the perpendicular line from $A$ to $BC$, and a median from $C$ to $AB$ is drawn that extends to intersect the circumcircle of $\triangle ABC$ at $K$. Prove that $C, K, H,$ and $D$ are concyclic.

I am confused as to where to start, but I think this is proven by Angle chasing, as there aren't any lengths we can find that pop out immediately hence drawing in $DK, KH, HC, CD$ to prove opposite angles sum to $180^{\circ}$.

Could someone please help me with this problem?

Answer 1

Actually, a power of a point approach can work. Let line $AD$ intersect $CK$ at $X$, the circumcircle of $\triangle CDK$ at $P$, and the circumcircle of $\triangle ABC$ at $Q$. Then, power of a point at $X$ gives $$XQ\cdot XA = XK\cdot XC = XP\cdot XD,$$ and computing $XQ$, $XA$, $XD$ in terms of $BC$ and $BH$ yields $XP = CH$. You can then show that $CHPD$ is an isosceles trapezoid, hence cyclic. Therefore the circumcircle of $\triangle CDP$ contains both $H$ (by the preceding sentence) and $K$ (by definition), so $C$, $D$, $H$, $K$ are concyclic.

Answer 2

In the picture (1) we have C coincident on H,N is coincident on A. So CN and AH are coincident.

Now we keep BC fixed and move AD towards BC such that H locates in between B and C which is shown in picture (2). This is an affine transformation in which H leaves point C and N leaves point A. The extension of KH meets the circle at I.The transformation deserves the property of $CN||AI$ We have:

$CN||AI\rightarrow \overset{\large \frown}{AN}=\overset{\large \frown}{CI}\Rightarrow \widehat {CKI}=\widehat{AKN}=\widehat{ABN}$

In this way we have:

$\widehat{ABN}+\widehat{NBC}=\widehat{DKC}+\widehat{CKI}$

OR:

$\widehat{DKI}=\widehat{ABC}$

In parallelogram ABCD we have:

$\widehat{ABC}+\widehat {BCD}=180^o$

Which results in:

$\widehat{DKI}+\widehat {BCD}=180^o$

$\widehat{BCD}=\widehat{HCD}$

Which deduces that quadrilateral DCHK is cyclic.

Answer 3

The green circle AHB (with E as center and AEB as diameter) will cut DA extended at Q. Thus, AHBQ is cyclic with $\angle AQB = 90^0$. This forces AHBQ to be a rectangle with HEQ as another diagonal of that quadrilateral.

Then, $\angle 1= \angle 2= \angle 3$ and $\angle 2 = \angle 4$. This means $\angle 5 = \angle 6$.

By considering the blue circle ACBK, we have $\angle 6 = \angle 7$. Then, $\angle DQK = \angle 3 + \angle 5 = \angle 1 + \angle 7 = \angle KCZ$. This means DCKQ is cyclic.

$\angle DQH = \angle 3 = \angle 1 = \angle HCZ$. This means DCHQ is also cyclic.

Result follows by combining the last two results.