3

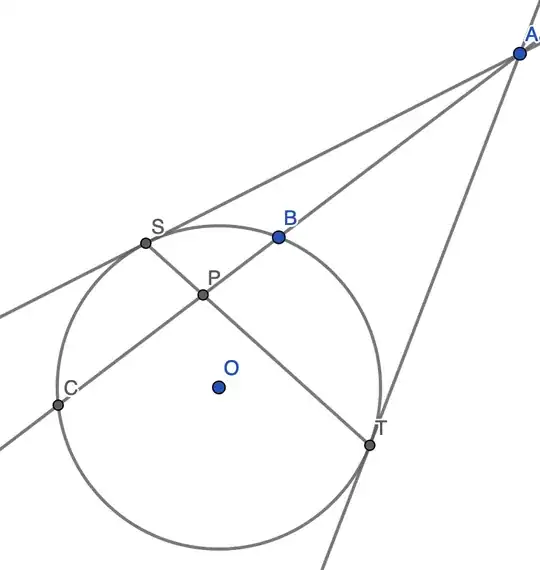
Let point $A$ be outside of circle $O$, where a secant through $A$ intersects $O$ at $ B $ and $ C $ where $ B $ is between $ A $ and $C$. The two tangents from $A$ touch $O$ at $S$ and $T$. Let $AC$ intersect $ST$ at $P$.

Prove that $\frac{AP}{PC} = 2\cdot \frac{AB}{BC}$

I think the most straighforward way is to use Power of a point to solve this question. So that $SP \cdot PT = BP \cdot PC$ and ${AS}^2 = AB\cdot BC = AT^2$.

An anyone help me finish from here, since I have not found a relation yet?

Thanks in advance

enter image description here

Tim Macdonald
  • 109

1 Answers1

3

Admittedly doesn't use power of a point much, but a neat trick is to draw the midpoint $M$ of segment $BC$ to get rid of the coefficient of $2$, so that the desired equality becomes $$\frac{AP}{PC} = \frac{AB}{BC/2} = \frac{AB}{BM} \iff \frac{AC}{AP} = 1 + \frac{PC}{AP} = 1 + \frac{BM}{AB} = \frac{AM}{AB}.$$ This rearranges to $AP\cdot AM = AB\cdot AC$. One way to finish from here is to show that $\triangle APT\sim\triangle ATM$ (using the fact that $A$, $M$, $O$, $S$, and $T$ lie on the circle with diameter $AO$) and $\triangle ABT\sim\triangle ATC$. Alternatively, you can do some algebraic manipulation to $PM\cdot PA = PS\cdot PT = PB\cdot PC$ (which again follows from $A$, $M$, $S$, $T$ being concyclic and power of a point) to recover $AP\cdot AM = AB\cdot AC$.

Aditya Pahuja
  • 86